







公式①:
公式②:
公式③:
公式④:
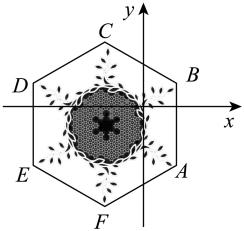
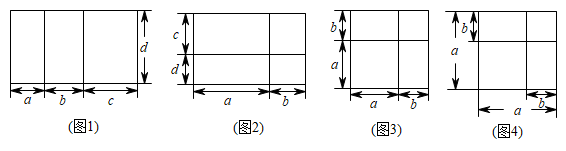
图1对应公式,图2对应公式,图3对应公式,图4对应公式;
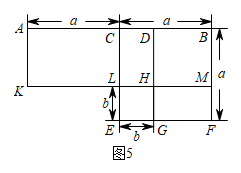
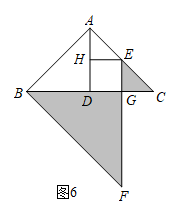
①若E为边AC的中点,则的值为 ▲ ;
②若E不为边AC的中点时,试问①中的结论是否仍成立?若成立,写出证明过程;若不成立,请说明理由.

如图1,中,
,
, 点D是
上一点,连接
, 以
为一边作
, 使
,
, 连接
,
与
的数量关系,位置关系.
如图2,中,
,
, 点M是
上一点,点D是
上一点,连接
, 以
为一边作
, 使
,
, 连接
, 求
的度数.
如图3,中,
,
,
, 点M是
中点,点D是
上一点且
, 连接
, 以
为一边作
, 使
,
, 连接
, 求
的长.