浙教版备考2023年中考数学一轮复习86.概率及其应用

更新时间：2023-01-01 浏览次数：104 类型：一轮复习

一、单选题（每题3分，共30分）

1. (2024·贵州模拟) 下列说法中错误的是（　　）

A . 随机事件发生的概率大于0，小于1 B . 概率很小的事件不可能发生 C . 必然事件发生的概率为1 D . 不可能事件发生的概率为0

答案解析收藏纠错 + 选题
2. (2024七下·沈阳月考) 下列说法正确的是（）

A . 自然现象中，“太阳东方升起”是必然事件 B . 成语“水中捞月”所描述的事件，是随机事件 C . “襄阳明天降雨的概率为0.6”，表示襄阳明天一定降雨 D . 若抽奖活动的中奖概率为 $\text{[math]}$ ，则抽奖50次必中奖1次

答案解析收藏纠错 + 选题
3. (2024七下·泰山期中) “14人中至少有2人在同一个月过生日”这一事件发生的概率为P，则（）

A . P＝0 B . 0＜P＜1 C . P＝1 D . P＞1

答案解析收藏纠错 + 选题
4. (2024九下·河口模拟) 无色酚酞溶液是一中常见常用酸碱指示剂，广泛应用于检验溶液酸碱性，通常情况下酚酞溶液遇酸溶液不变色，遇中性溶液也不变色，遇碱溶液变红色．现有5瓶缺失标签的无色液体：蒸馏水、白醋溶液、食用碱溶液、柠檬水溶液、火碱溶液，将酚酞试剂滴入任意一瓶液体后呈现红色的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022九上·襄汾月考) 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，并绘制了如下表格．则该结果发生的概率约为（）
实验次数
100
500
1000
2000
4000
频率
0.37
0.32
0.345
0.339
0.333

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·益阳) 在某市组织的物理实验操作考试中，考试所用实验室共有24个测试位，分成6组，同组4个测试位各有一道相同试题，各组的试题不同，分别标记为A，B，C，D，E，F，考生从中随机抽取一道试题，则某个考生抽到试题A的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·绵阳) 某校开展岗位体验劳动教育活动，设置了“安全小卫士”“环卫小卫士”“图书管理小卫士”“宿舍管理小卫士”共四个岗位，每个岗位体验人数不限且每位同学只能从中随机选择一个岗位进行体验、甲、乙两名同学都参加了此项活动，则这两名同学恰好在同一岗位体验的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·丛台月考) 一个不透明的口袋中装有红球6个，黄球9个，绿球3个，这些球除颜色外没有其他任何区别．现从中任意摸出一个球．如果要使摸到绿球的概率为 $\text{[math]}$ ，需要在这个口袋中再放入绿球(　　)个

A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
9. 不透明的布袋中，装有红、黄、白三种只有颜色不同的小球，其中红色小球有8个，黄、白色小球的数目相同。为估计袋中黄色小球的数目，每次将袋中小球搅匀后摸出一个小球记下颜色，再次搅匀……多次试验发现摸到红球的频率是 $\text{[math]}$ ，则估计黄色小球的数目是（）

A . 2个 B . 20个 C . 40个 D . 48个

答案解析收藏纠错 + 选题
10. (2022·徐州) 将一枚飞镖任意投掷到如图所示的正六边形镖盘上，若飞镖落在镖盘上各点的机会相等，则飞镖落在阴影区域的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题4分，共18分）

11. (2023·抚顺模拟) 如图，一个质地均匀的正五边形转盘，指针的位置固定，当转盘自由转动停止后，观察指针指向区域内的数（若指针正好指向分界线，则重新转一次），这个数是一个奇数的概率是.

答案解析收藏纠错 + 选题
12. (2022·攀枝花) 盒子里装有除颜色外，没有其他区别的2个红球和2个黑球，搅匀后从中取出1个球，放回搅匀再取出第2个球，则两次取出的球是1红1黑的概率为.

答案解析收藏纠错 + 选题
13. (2022·六盘水) 将一副去掉大小王的扑克牌平均分发给甲、乙、丙、丁四人，已知甲有5张红桃牌，乙有4张红桃牌，那么丁的红桃牌有种不同的情况．

答案解析收藏纠错 + 选题
14. (2024九下·禹城模拟) 一个不透明的口袋中装有5个红球和 $\text{[math]}$ 个黄球，这些球除颜色外都相同，某同学进行了如下试验：从袋中随机摸出1个球记下它的颜色后，放回摇匀，为一次摸球试验．根据记录在下表中的摸球试验数据，可以估计出 $\text{[math]}$ 的值为．
摸球的总次数 $\text{[math]}$
100
500
1000
2000
…
摸出红球的次数 $\text{[math]}$
19
101
199
400
…
摸出红球的频率 $\text{[math]}$
0.190
0.202
0.199
0.200
…

答案解析收藏纠错 + 选题
15. (2020九上·大邑期中) 已知a、b、c、满足 $\text{[math]}$ ，从下列四点：① $\text{[math]}$ ；②(2，1)；③ $\text{[math]}$ ；④(1，﹣1)，中任意取一点恰好在正比例函数y＝kx图象上的概率是.

答案解析收藏纠错 + 选题
16. (2023九上·越城月考) 一个密码箱的密码，每个数位上的数都是从0到9的自然数，若要使不知道密码的人一次就拨对密码的概率小于 $\text{[math]}$ ，则密码的位数至少需要位．

答案解析收藏纠错 + 选题

三、解答题（共10题，共72分）

17. (2022·盐城) 某社区举行新冠疫情防控核酸检测大演练，卫生防疫部门在该社区设置了三个核酸检测点A、B、C，甲、乙两人任意选择一个检测点参加检测．求甲、乙两人不在同一检测点参加检测的概率．（用画树状图或列表的方法求解）

答案解析收藏纠错 + 选题
18. (2022七下·濮阳期末) 幻方是一种将数字排在正方形格子中，使每行、每列和每条对角线上的数字和都相等的模型.数学课上，老师在黑板上画出一个幻方如图所示，并设计游戏：一人将一颗能粘在黑板上的磁铁豆随机投入幻方内，另一人猜数，若所猜数字与投出的数字相符，则猜数的人获胜，否则投磁铁豆的人获胜.猜想的方法从以下两种中选一种：

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Ⅰ.猜“是大于 $\text{[math]}$ 的数”或“不是大于 $\text{[math]}$ 的数”；
Ⅱ.猜“是 $\text{[math]}$ 的倍数”或“不是 $\text{[math]}$ 的倍数”；如果轮到你猜想，那么为了尽可能获胜，你将选择哪一种猜数方法？怎么猜？为什么？

答案解析收藏纠错 + 选题
19. (2022·巴中) 为扎实推进“五育并举”工作，某校利用课外活动时间开设了舞蹈、篮球、围棋和足球四个社团活动，每个学生只选择一项活动参加．为了解活动开展情况，学校随机抽取部分学生进行调查，将调查结果绘成如下表格和扇形统计图．
参加四个社团活动人数统计表
社团活动
舞蹈
篮球
围棋
足球
人数
50
30
80
参加四个社团活动人数扇形统计图
请根据以上信息，回答下列问题：
1. （1）抽取的学生共有人，其中参加围棋社的有人；
2. （2）若该校有3200人，估计全校参加篮球社的学生有多少人？
3. （3）某班有3男2女共5名学生参加足球社，现从中随机抽取2名学生参加学校足球队，请用树状图或列表法说明恰好抽到一男一女的概率．
答案解析收藏纠错 + 选题
20. (2022·岳阳) 守护好一江碧水，打造长江最美岸线.江豚，麋鹿，天鹅已成为岳阳“吉祥三宝”的新名片.某校生物兴趣小组设计了3张环保宣传卡片，正面图案如图所示，它们除此之外完全相同.
1. （1）将这3张卡片背面朝上，洗匀，从中随机抽取一张，则抽取的卡片正面图案恰好是“麋鹿”的概率为；
2. （2）将这3张卡片背面朝上，洗匀，从中随机抽取一张，不放回，再从剩余的两张卡片中随机抽取一张，请用列表或画树状图的方法，求抽取的卡片正面图案恰好是“江豚”和“天鹅”的概率.
答案解析收藏纠错 + 选题
21. (2023·会宁模拟) 第24届冬季奥林匹克运动会于2022年2月4至20日在我国北京-张家口成功举办，其中张家口赛区设有四个冬奥会竞赛场馆，分别为：A.云顶滑雪公园、B.国家跳台滑雪中心、C.国家越野滑雪中心、D.国家冬季两项中心.小明和小颖都是志愿者，他们被随机分配到这四个竞赛场馆中的任意一个场馆的可能性相同.
1. （1）小明被分配到D.国家冬季两项中心场馆做志愿者的概率是多少？
2. （2）利用画树状图或列表的方法，求小明和小颖被分配到同一场馆做志愿者的概率.
答案解析收藏纠错 + 选题
22. (2022·云南) 某班甲、乙两名同学被推荐到学校艺术节上表演节目，计划用葫芦丝合奏一首乐曲，要合奏的乐曲是用游戏的方式在《月光下的凤尾竹》与《彩云之南》中确定一首．
游戏规则如下：在—个不透明的口袋中装有分别标有数字1，2，3，4的四个小球（除标号外，其余都相同），甲从口袋中任意摸出1个小球，小球上的数字记为a．在另一个不透明的口袋中装有分别标有数字1，2的两张卡片（除标号外，其余都相同），乙从口袋里任意摸出1张卡片卡片上的数字记为b．然后计算这两个数的和，即a+b，若a+b为奇数，则演奏《月光下的凤尾竹》，否则，演奏（彩云之南》．
1. （1）用列表法或画树状图法中的一种方法，求（a，b）所有可能出现的结果总数；
2. （2）你认为这个游戏公平不？如果公平，请说明理由；如果不公平，哪一首乐曲更可能被选中？
答案解析收藏纠错 + 选题

23. (2022九上·南海月考) 一只不透明袋子中装有1个白球和若干个红球，这些球除颜色外都相同，某课外学习小组做摸球试验：将球搅匀后从中任意摸出1个球，记下颜色后放回、搅匀，不断重复这个过程，获得数据如下：

摸球的次数	200	300	400	1000	1600	2000
摸到白球的频数	72	93	130	334	532	667
摸到白球的频率	0.3600	0.3100	0.3250	0.3340	0.3325	0.3335

（1）该学习小组发现，随着摸球次数的增多，摸到白球的频率在一个常数附近摆动，请直接写出这个常数（精确到0.01），由此估出红球有几个？
（2）在这次摸球试验中，从袋中随机摸出1个球，记下颜色后放回，再从中随机摸出1个球，利用画树状图或列表的方法表示所有可能出现的结果，并求两次摸到的球恰好1是个白球，1个是红球的概率．

答案解析收藏纠错 + 选题

24. (2021·集美模拟) 如图是某校校史荣誉室的正方形网格平面图，实线表示墙体或门.在点 $\text{[math]}$ 处安装了360度旋转摄像头，由于墙体的的遮挡，阴影部分无法监控，这部分无法监控到的区域通常称为监控盲区.
1. （1）小红同学进入校史荣誉室随意参观，站在监控盲区的概率是多少？
2. （2）为了监控效果更好，使得监控盲区最小，请你帮助学校在墙体 $\text{[math]}$ 上重新设计摄像头安装的位置，画出示意图，并说明理由.
答案解析收藏纠错 + 选题
25. (2022·六盘水) 为倡导“全民健身，健康向上”的生活方式，我市教育系统特举办教职工气排球比赛．比赛采取小组循环，每场比赛实行三局两胜制，取实力最强的两支队伍参加决赛，从C组的比分胜负表中知道二中胜4场负1场．
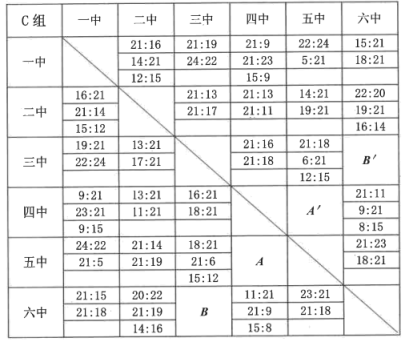
教职工气排球比赛比分胜负表
1. （1）根据表中数据可知，一中共获胜场，“四中VS五中”的比赛获胜可能性最大的是；
2. （2）若 $\text{[math]}$ 处的比分是21∶10和21∶8，并且参加决赛的队伍是二中和五中，则 $\text{[math]}$ 处的比分可以是和；（两局结束比赛，根据自己的理解填写比分）；
3. （3）若 $\text{[math]}$ 处的比分是10∶21和8∶21， $\text{[math]}$ 处的比分是21∶18，15∶21，15∶12，那么实力最强的是哪两支队伍，请说明理由．
答案解析收藏纠错 + 选题

26. (2022·乐山模拟) 某大学为了解大学生对中国共产党党史知识的学习情况，在大学一年级和二年级举行有关党史知识测试活动，现从一二两个年级中各随机抽取20名学生的测试成绩（满分50分，30分及30分以上为合格：40分及40分以上为优秀）进行整理、描述和分析，给出了下面的部分信息．

大学一年级20名学生的测试成绩为：39，50，39，50，49，30，30，49，49，49，43，43，43，37，37，37，43，43，37，25

大学二年级20名学生的测试成绩条形统计图如下图所示；两个年级抽取的学生的测试成绩的平均数、众数、中位数、优秀率如表所示：

年级	平均数	众数	中位数	优秀率
大一	a	b	43	m
大二	39.5	44	c	n

请你根据上面提供的所有信息，解答下列问题：

（1）上表中a＝ ▲ ， b＝ ▲ ， c＝ ▲ ， m＝ ▲ ， n ▲ ；根据样本统计数据，你认为该大学一、二年级中哪个年级学生掌握党史知识较好？并说明理由（写出一条理由即可）；
（2）已知该大学一、二年级共1240名学生参加了此次测试活动，通过计算，估计参加此次测试活动成绩合格的学生人数能否超过1000人；
（3）从样本中测试成绩为满分的一、二年级的学生中随机抽取两名学生，用列举法求两人在同一年级的概率．

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙教版备考2023年中考数学一轮复习86.概率及其应用

副标题：

*注意事项：

浙教版备考2023年中考数学一轮复习86.概率及其应用

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

摸球的总次数 $\text{[math]}$	100	500	1000	2000	…
摸出红球的次数 $\text{[math]}$	19	101	199	400	…
摸出红球的频率 $\text{[math]}$	0.190	0.202	0.199	0.200	…

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

实验次数	100	500	1000	2000	4000
频率	0.37	0.32	0.345	0.339	0.333

社团活动	舞蹈	篮球	围棋	足球
人数	50	30		80