用含
的代数式表示:
▲ ;
▲ ;当
为何值时,
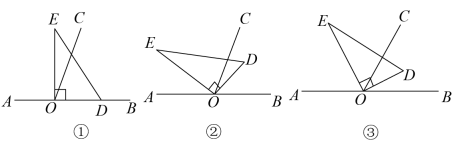
从三角尺
与三角尺
第一对直角边和斜边重叠开始起到另一对直角边和斜边重叠结束止,经过的时间
为 ▲ 秒
①若旋转时间
时,则
▲ ;
②若平分
平分
, 求
的值;

如图3,继续旋转三角板 , 使得
、
同时在直线
的右侧,请问上面的数量关系是否仍然成立?并说明理由.
试用字母
分别表示
与
;
在旋转的过程中,当
为何值时
平分
.
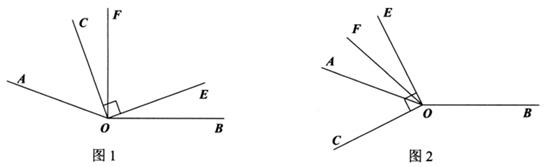
①探究(小于平角)和
的度数之间的关系,写出你的结论,并说明理由.
②在(小于平角)的内部有一条射线OF,满足:
, 试确定
与
的之间的数量关系,并说明理由.


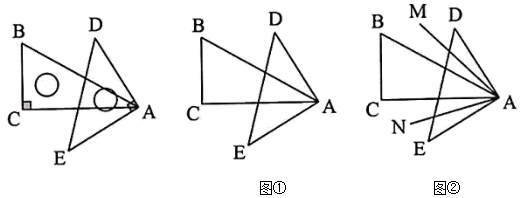

①在旋转过程中,若 , 求
得度数;
②在旋转过程中,与
有怎样的数量关系?请依据图②说明理由.