 B .
B .  C .
C .  D .
D . 

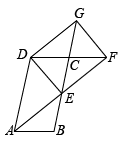
①四边形是平行四边形;
②当时,四边形
是矩形;
③当时,四边形
是菱形;
④当 , 且
时,四边形
是正方形.
其中正确结论有(填上所有正确结论的序号).

①;
②若 , 则
;
③若点 ,
在抛物线上,
, 且
, 则
;
④当时,关于
的一元二次方程
必有两个不相等的实数根.
其中正确的是(填写序号).
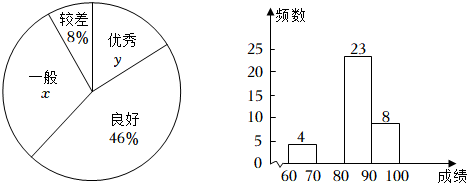
请根据统计图提供的信息,回答如下问题:
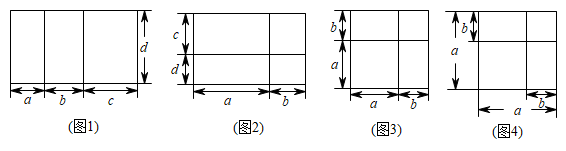
公式①:
公式②:
公式③:
公式④:
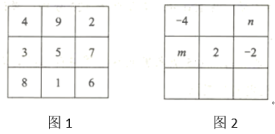
图1对应公式,图2对应公式,图3对应公式,图4对应公式;
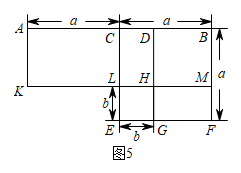
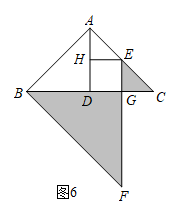
①若E为边AC的中点,则的值为 ▲ ;
②若E不为边AC的中点时,试问①中的结论是否仍成立?若成立,写出证明过程;若不成立,请说明理由.
①当与x轴平行时,求
的值;
②当与x轴不平行时,求
的最大值;