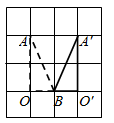
 B .
B . 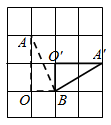 C .
C . 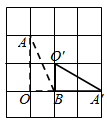 D .
D . 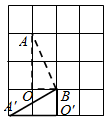
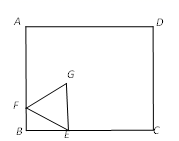



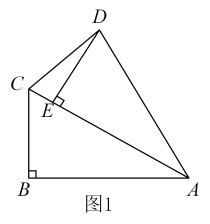
如图①,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE′(点A的对应点为点C).延长AE交CE′于点F,连接DE.

试判断四边形BE'FE的形状,并说明理由;
如图①,若AB=4,当BE的长为时,△ADE为等腰三角形,请直接写出结果.

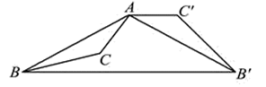
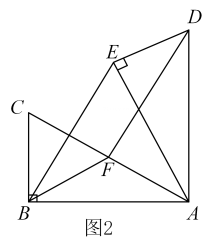
①在旋转过程中,当∠是直角时,求
的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)
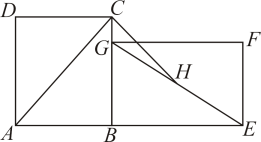
②若正方形ABCD的边长为1,在旋转过程中,求长的最大值和此时
的度数,直接写出结果不必说明理由.


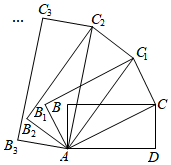
答:_(填“一致”或“不一致”).