2023年浙教版数学八年级上册2.4 等腰三角形的判定定理 ...

更新时间：2023-07-10 浏览次数：69 类型：同步测试

一、选择题

1. (2023·随州模拟) 如图，等边三角形ABC， $\text{[math]}$ ， D为BC中点，M为AD上的动点，连接CM，将线段CM绕点C逆时针方向旋转60°得到CN，连接ND，则 $\text{[math]}$ 的最小值为（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . 6

答案解析收藏纠错 + 选题
2. (2023八下·渠县月考) 如图，过边长为1的等边三角形ABC的边AB上一点P，作 $\text{[math]}$ 于点E，Q为BC延长线上一点，当 $\text{[math]}$ 时，PQ交AC于点D，则DE的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 不能确定

答案解析收藏纠错 + 选题
3. (2022八上·平谷期末) 如图，等边 $\text{[math]}$ 和等边 $\text{[math]}$ 中，A、B、C三点共线， $\text{[math]}$ 和 $\text{[math]}$ 相交于点F，下列结论中正确的个数是（）
① $\text{[math]}$ ；② $\text{[math]}$ 平分 $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
4. (2023八上·平南期末) 如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作等边△ABC和等边△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ，下列结论错误的是（）

A . AD＝BE B . ∠DOE＝60° C . DE＝DP D . PQ∥AE

答案解析收藏纠错 + 选题
5. (2022八上·常熟月考) 如图等腰△ABC中，AB＝AC，∠BAC＝120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP＝OC，下面的结论：①∠APO+∠DCO＝30°；②△OPC是等边三角形；③AC＝AO+AP；④S_△_ABC＝S_四边形_AOCP ，其中正确的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
6. (2022·任城模拟) 如图， $\text{[math]}$ ，在 $\text{[math]}$ 上截取 $\text{[math]}$ ．过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径画弧，交 $\text{[math]}$ 于点 $\text{[math]}$ ；过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径画弧，交 $\text{[math]}$ 于点 $\text{[math]}$ ；按此规律，所得线段 $\text{[math]}$ 的长等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022九下·义乌月考) 如图，点P，Q，R分别在等边△ABC的三边上，且AP＝BQ＝CR，过点P，Q，R分别作BC，CA，AB边的垂线，得到△DEF．若要求△DEF的面积，则只需知道（）

A . AB的长 B . DP的长 C . BP的长 D . AP的长

答案解析收藏纠错 + 选题
8. (2023八上·潮南期末) 如图，等边 $\text{[math]}$ 中，D为AC中点，点P、Q分别为AB、AD上的点， $\text{[math]}$ ， $\text{[math]}$ ，在BD上有一动点E，则 $\text{[math]}$ 的最小值为（）

A . 7 B . 8 C . 10 D . 12

答案解析收藏纠错 + 选题

二、填空题

9. (2022八上·海港期末) 如图的5个三角形中，均有 $\text{[math]}$ ，则经过三角形的一个顶点的一条直线不能够将这个三角形分成两个小等腰三角形的是（填序号）.

答案解析收藏纠错 + 选题
10. (2022八下·埇桥期中) 如图， $\text{[math]}$ ，点A是BO延长线上的一点，OA＝10cm，动点P从点A出发沿AB以2cm/s的速度移动，动点Q从点O出发沿OC以1cm/s的速度移动，如果点P，Q同时出发，用t（s）表示移动的时间，当t＝时，△POQ是等腰三角形．

答案解析收藏纠错 + 选题
11. (2023八下·高州月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， D为 $\text{[math]}$ 的中点，P为 $\text{[math]}$ 上一动点，连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的最小值是.

答案解析收藏纠错 + 选题
12. (2022八上·长沙期中) 如图，△ABC为等边三角形，点D与点C关于直线AB对称，E，F分别是边BC和AC上的点，BE＝CF，AE与BF交于点G．DG交AB于点H．下列四个结论中：①△ABE≌△BCF；②AG+BG＝DG；③HG+GE＝GF；④△AHF为等边三角形．所有正确结论的序号是．

答案解析收藏纠错 + 选题
13. (2022·新昌模拟) 在△ABC中，∠A=60°，点P和点Q分别是边AC和BC上的两个动点，分别连结BP和PQ，把△ABC分割成三个三角形，若分割成的这三个三角形都是等腰三角形，则∠ABC的度数可以是.

答案解析收藏纠错 + 选题
14. (2021八上·南充期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，高 $\text{[math]}$ .作点H关于 $\text{[math]}$ ， $\text{[math]}$ 的对称点D，E，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点P，交 $\text{[math]}$ 于点Q；连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③五边形 $\text{[math]}$ 的面积是24；④ $\text{[math]}$ 的周长为6.其中正确结论是.（填写序号）

答案解析收藏纠错 + 选题

三、综合题

15. (2022八上·黄冈月考) 已知：在等边 $\text{[math]}$ 中，点 $\text{[math]}$ 是 $\text{[math]}$ 边所在直线上的一个动点（ $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 两点均不重合），点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ .
1. （1）如图①，当 $\text{[math]}$ 是 $\text{[math]}$ 边的中点时，求证： $\text{[math]}$ ；
2. （2）如图②，当 $\text{[math]}$ 是线段 $\text{[math]}$ 边上任意一点时，（1）中的结论是否一定成立？请说明理由；
3. （3）若点 $\text{[math]}$ 是线段 $\text{[math]}$ 的延长线上任一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
16. (2022八上·浦城期中) 阅读下列材料，解答问题：
定义：线段BM把等腰△ABC分成△ABM与△BCM（如图1），如果△ABM与△BCM均为等腰三角形，那么线段BM叫做△ABC的完美分割线.
1. （1）如图1，已知△ABC中， $\text{[math]}$ ， BM为△ABC的完美分割线，且 $\text{[math]}$ ，则 $\text{[math]}$ °， $\text{[math]}$ °；
2. （2）如图2，已知△ABC中， $\text{[math]}$ ，求证：AN为△ABC的完美分割线；
3. （3）如图3，已知△ABC是一等腰三角形纸片，AB＝AC，AN是它的一条完美分割线，且 $\text{[math]}$ ，将△ACN沿直线AN折叠后，点C落在点 $\text{[math]}$ 处， $\text{[math]}$ 交BN于点M.求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题
17. (2023八上·东阳月考) 概念学习
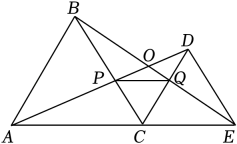
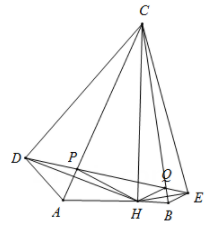
规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”.

从三角形 $\text{[math]}$ 不是等腰三角形 $\text{[math]}$ 一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”.
1. （1）理解概念
  如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，请写出图中两对“等角三角形”
2. （2）概念应用
  如图2，在 $\text{[math]}$ 中， $\text{[math]}$ 为角平分线， $\text{[math]}$ ， $\text{[math]}$ .
  求证： $\text{[math]}$ 为 $\text{[math]}$ 的等角分割线.
3. （3）在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的等角分割线，直接写出 $\text{[math]}$ 的度数.
答案解析收藏纠错 + 选题

18. (2022八下·太原期末) 综合与实践：

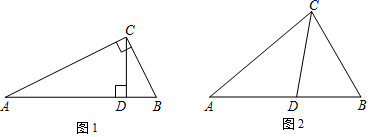
已知，等腰三角形纸片ABC中，AB＝AC，∠BAC＝36°．现要将其剪成三张小纸片，使每张小纸片都是等腰三角形（不能有剩余）．下面是小文借助尺规解决这一问题的过程，请阅读后完成相应任务．

作法：如图1所示，

①分别作AB，AC的垂直平分线，交于点P；

②连接PA，PB，PC．

结论：沿线段PA，PB，PC剪开，即可得到三个等腰三角形，

理由：∵点P在线段AB的垂直平分线上，

∴…….. （依据）．

同理，PA＝PC．

∴PA＝PB＝PC．

∴△PAB、△PBC、△PAC都是等腰三角形

任务：

（1）上述过程中，横线上的结论为，括号中的依据为．
（2）受小文的启发，同学们想到另一种思路：如图2，以B为圆心，BC长为半径画弧，交AC于点D，交AB于点E．在此基础上构造两条线段（以图中标有字母的点为端点）作为裁剪线，也可解决问题！请在图2中画出一种裁剪方案，直接写出得到的三个等腰三角形及相应顶角的度数．
（3）如图3，等腰三角形纸片ABC中，AB＝AC，∠BAC＝108°，请从A，B两题中任选一题作答、我选择题．
A．请在图3中设计出一种裁剪方案，将该三角形纸片分成三个等腰三角形（要求：尺规作图，保留作图痕迹，不写作法，说明裁剪线）．
B．请在图3中设计出一种裁剪方案，将该三角形纸片分成四个等腰三角形，且四个三角形互不全等（要求：尺规作图，保留作图痕迹，不写作法，说明裁剪线）．

答案解析收藏纠错 + 选题

19. (2023八上·桂平期末) 如图，已知点D是等边三角形 $\text{[math]}$ 中 $\text{[math]}$ 边所在直线上的点，连接 $\text{[math]}$ ，过点D作 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的邻补角的平分线交于点F.
1. （1）如图①，当点D在线段 $\text{[math]}$ 上时，过点D作 $\text{[math]}$ ，且交 $\text{[math]}$ 于点E.求证： $\text{[math]}$ ；
2. （2）如图①，在（1）的条件下，求证： $\text{[math]}$ ；
3. （3）如图②，当点D在线段 $\text{[math]}$ 的延长线上时，（2）中线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系式还成立吗？若成立，请加以证明；若不成立，请写出线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间新的数量关系式，并说明理由.
答案解析收藏纠错 + 选题
20. (2021八上·遵义期末) 在边长为8的等边三角形 $\text{[math]}$ 中，点Q是BC上一点，点P是AB上一动点，点P以1个单位每秒的速度从点A向点B移动，设运动时间为t秒.
1. （1）如图1，若 $\text{[math]}$ ，当t取何值时 $\text{[math]}$ ？
2. （2）若点P从点A向点B运动，同时点Q以2个单位的速度从点B经点C向点A运动，当t为何值时， $\text{[math]}$ 为等边三角形（在图2中画出示意图）.
3. （3）如图3，将边长为 $\text{[math]}$ 的等边三角形 $\text{[math]}$ 变换为AB，AC为腰，BC为底的等腰三角形，且 $\text{[math]}$ ， $\text{[math]}$ ，点P运动到AB中点处静止后，点M，N分别为BC，AC上动点，点M以1个单位每秒的速度从点B向C运动，同时点N以a个单位每秒的速度从点C向A运动，当 $\text{[math]}$ ， $\text{[math]}$ 全等时，直接写出a的值.
答案解析收藏纠错 + 选题