2023年中考数学真题分类汇编（全国版）：三角形（9）

第一步，如图①将纸片对折，使AB与DC重合，折痕为EF，展开后如图②；

第二步，再将图②中的纸片沿对角线BD折叠，展开后如图③；

第三步，将图③中的纸片沿过点E的直线折叠，使点C落在对角线BD上的点H处，如图④．
则DH的长为（    ）

如图1，数学实践课上，学习小组进行探究活动，老师要求大家对矩形进行如下操作：①分别以点为圆心，以大于的长度为半径作弧，两弧相交于点 ， ， 作直线交于点 ， 连接；②将沿翻折，点的对应点落在点处，作射线交于点 ．

【问题提出】

在矩形中， ， 求线段的长．

【问题解决】

经过小组合作、探究、展示，其中的两个方案如下：

方案一：连接 ， 如图2．经过推理、计算可求出线段的长；

方案二：将绕点旋转至处，如图3．经过推理、计算可求出线段的长．

请你任选其中一种方案求线段的长．

用直尺和圆规，作的垂直平分线交于点E，交于点F，垂足为点O．（只保留作图痕迹）

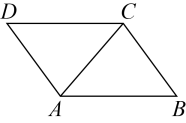
已知：如图，四边形是平行四边形，是对角线，垂直平分 ， 垂足为点O．

求证： ．

证明：∵四边形是平行四边形，

∴ ．

∴            ▲             ．

∵垂直平分 ，

∴            ▲             ．

又            ▲             ．

∴ ．

∴ ．

小虹再进一步研究发现，过平行四边形对角线中点的直线与平行四边形一组对边相交形成的线段均有此特征．请你依照题意完成下面命题：

过平行四边形对角线中点的直线            ▲             ．

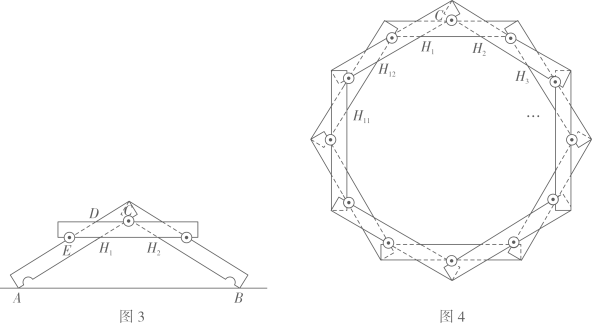
探究1：图3是“桥”侧面示意图，A，B为横梁与地面的交点，C，E为圆心，D，H₁ ， H₂是横梁侧面两边的交点.测得AB=32cm，点C到AB的距离为12cm.试判断四边形CDEH₁的形状，并求的值.

探究2：若搭成的“桥”刚好能绕成环，其侧面示意图的内部形成一个多边形.

①若有12根横梁绕成环，图4是其侧面示意图，内部形成十二边形 ， 求的值；

②若有n根横梁绕成的环（n为偶数，且n≥6），试用关于n的代数式表示内部形成的多边形的周长.

在中， ， ， D是AB边上一点，且（n为正整数），E是AC边上的动点，过点D作DE的垂线交直线BC于点F.

阅读材料：

如图1，四边形是矩形，是等腰直角三角形，记为、为 ， 若 ， 则 ．

证明：设 ， ∵ ， ∴ ，

易证

∴ ，

∴

∴ ，

若时，当 ， 则 ．

同理：若时，当 ， 则 ．

根据上述材料，完成下列问题：

如图2，直线与反比例函数的图象交于点 ， 与轴交于点 ． 将直线绕点顺时针旋转后的直线与轴交于点 ， 过点作轴于点 ， 过点作轴于点 ， 已知 ．