2023年中考数学真题分类汇编（全国版）：圆（2）

更新时间：2023-07-23 浏览次数：101 类型：二轮复习

一、选择题

1. (2023·新疆) 如图，在 $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，则扇形 $\text{[math]}$ (阴影部分)的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·遂宁) 为增强班级凝聚力，吴老师组织开展了一次主题班会．班会上，他设计了一个如图的飞镖靶盘，靶盘由两个同心圆构成，小圆半径为 $\text{[math]}$ ，大圆半径为 $\text{[math]}$ ，每个扇形的圆心角为60度．如果用飞镖击中靶盘每一处是等可能的，那么小全同学任意投掷飞镖1次（击中边界或没有击中靶盘，则重投1次），投中“免一次作业”的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023·宜宾) 如图，已知点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ 为 $\text{[math]}$ 的中点．若 $\text{[math]}$ ，则 $\text{[math]}$ 等于（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·凉山) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 1 B . 2 C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
5. (2023·泸州) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在斜边 $\text{[math]}$ 上，以 $\text{[math]}$ 为直径的半圆 $\text{[math]}$ 与 $\text{[math]}$ 相切于点 $\text{[math]}$ ，与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

6. (2023·烟台) 如图，将一个量角器与一把无刻度直尺水平摆放，直尺的长边与量角器的外弧分别交于点A，B，C，D，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
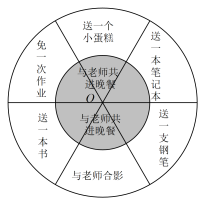
7. (2023·武威) 如图1，我国是世界上最早制造使用水车的国家.1556年兰州人段续的第一架水车创制成功后，黄河两岸人民纷纷仿制，车水灌田，水渠纵横，沃土繁丰．而今，兰州水车博览园是百里黄河风情线上的标志性景观，是兰州“水车之都”的象征．如图2是水车舀水灌溉示意图，水车轮的辐条（圆的半径） $\text{[math]}$ 长约为6米，辐条尽头装有刮板，刮板间安装有等距斜挂的长方体形状的水斗，当水流冲动水车轮刮板时，驱使水车徐徐转动，水斗依次舀满河水在点 $\text{[math]}$ 处离开水面，逆时针旋转 $\text{[math]}$ 上升至轮子上方 $\text{[math]}$ 处，斗口开始翻转向下，将水倾入木槽，由木槽导入水渠，进而灌溉，那么水斗从 $\text{[math]}$ 处（舀水）转动到 $\text{[math]}$ 处（倒水）所经过的路程是米．（结果保留 $\text{[math]}$ ）

答案解析收藏纠错 + 选题
8. (2023·温州) 若扇形的圆心角为 $\text{[math]}$ ，半径为18，则它的弧长为。

答案解析收藏纠错 + 选题
9. (2023·绍兴) 如图，四边形 $\text{[math]}$ 内接于圆 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是.

答案解析收藏纠错 + 选题
10. (2023·扬州) 用半径为 $\text{[math]}$ ，面积为 $\text{[math]}$ 的扇形纸片，围成一个圆锥的侧面，则这个圆锥的底面圆的半径为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2023·宁波) 如图，圆锥形烟囱帽的底面半径为 $\text{[math]}$ ，母线长为 $\text{[math]}$ ，则烟囱帽的侧面积为 $\text{[math]}$ ．（结果保留 $\text{[math]}$ ）

答案解析收藏纠错 + 选题
12. (2023·温州) 图1是 $\text{[math]}$ 方格绘成的七巧板图案，每个小方格的边长为 $\text{[math]}$ ，现将它前拼成一个“房子”造型（如图2），过左侧的三个端点作圆，并在圆内右侧部分留出矩形CDEF作为题字区域（点A，E，D，B在圆上，点C，F在AB上），形成一幅装饰画，则圆的半径为.若点A，N，M在同一直线上， $\text{[math]}$ ，则题字区域的面积为.

答案解析收藏纠错 + 选题

三、作图题

13. (2023·连云) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 为直径的 $\text{[math]}$ 交边 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ .
1. （1）请用无刻度的直尺和圆规作图：过点 $\text{[math]}$ 作 $\text{[math]}$ 的切线，交 $\text{[math]}$ 于点 $\text{[math]}$ ；（不写作法，保留作图痕迹，标明字母）
2. （2）在（1）的条件下，求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题

四、综合题

14. (2023·枣庄) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径，点C是 $\text{[math]}$ 的中点，过点C做射线 $\text{[math]}$ 的垂线，垂足为E．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 切线；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长；
3. （3）在（2）的条件下，求阴影部分的面积（用含有 $\text{[math]}$ 的式子表示）．
答案解析收藏纠错 + 选题
15. (2023·苏州) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的内接三角形， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上，连接 $\text{[math]}$ 并延长，交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，作 $\text{[math]}$ ，垂足为 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
16. (2023·天津市) 在 $\text{[math]}$ 中，半径 $\text{[math]}$ 垂直于弦 $\text{[math]}$ ，垂足为D， $\text{[math]}$ ， E为弦 $\text{[math]}$ 所对的优弧上一点．
1. （1）如图①，求 $\text{[math]}$ 和 $\text{[math]}$ 的大小；
2. （2）如图②， $\text{[math]}$ 与 $\text{[math]}$ 相交于点F， $\text{[math]}$ ，过点E作 $\text{[math]}$ 的切线，与 $\text{[math]}$ 的延长线相交于点G，若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
17. (2023·新疆) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，点 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
18. (2023·怀化) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，点 $\text{[math]}$ 是 $\text{[math]}$ 外一点， $\text{[math]}$ 与 $\text{[math]}$ 相切于点 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 上的一点．连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 为 $\text{[math]}$ 的切线；
2. （2）延长 $\text{[math]}$ 与 $\text{[math]}$ 的延长线交于点D，求证： $\text{[math]}$ ；
3. （3）若 $\text{[math]}$ ，求阴影部分的面积．
答案解析收藏纠错 + 选题
19. (2023·温州) 如图1，AB为半圆 $\text{[math]}$ 的直径， $\text{[math]}$ 为BA延长线上一点，CD切半圆于点 $\text{[math]}$ ，交CD延长线于点 $\text{[math]}$ ，交半圆于点 $\text{[math]}$ ，已知 $\text{[math]}$ .如图2，连结AF，P为线段AF上一点，过点 $\text{[math]}$ 作BC的平行线分别交CE，BE于点M，N，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ .设 $\text{[math]}$ .
1. （1）求CE的长和 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式.
2. （2）当 $\text{[math]}$ ，且长度分别等于 $\text{[math]}$ ， $\text{[math]}$ 的三条线段组成的三角形与 $\text{[math]}$ 相似时，求 $\text{[math]}$ 的值.
3. （3）延长 $\text{[math]}$ 交半圆 $\text{[math]}$ 于点 $\text{[math]}$ ，当 $\text{[math]}$ 时，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
20. (2023·台州) 我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系，用直线上点的位置刻画圆上点的位置，如图，AB是 $\text{[math]}$ 的直径，直线l是 $\text{[math]}$ 的切线，B为切点．P，Q是圆上两点（不与点A重合，且在直径AB的同侧），分别作射线AP，AQ交直线l于点C，点D．
1. （1）如图1，当 $\text{[math]}$ ， $\text{[math]}$ 长为 $\text{[math]}$ 时，求BC的长．
2. （2）如图2，当 $\text{[math]}$ ， $\text{[math]}$ 时，求 $\text{[math]}$ 的值．
3. （3）如图3，当 $\text{[math]}$ ， $\text{[math]}$ 时，连接BP，PQ，直接写出 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题