![]()
 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 
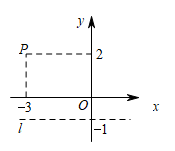

![]()
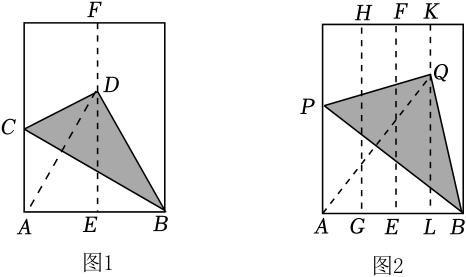
① 当点落在
轴上时,求点
的坐标;
② 若△为直角三角形,求点
的坐标.

图1是由四个全等的直角三角形围成的一个大正方形,中间的部分是一个小正方形(阴影).如果直角三角形较小的直角边长为a,较大的直角边长为b,斜边长为c,请你根据图1证明勾股定理;
如图2,圆柱的底面半径为 , 高为
, 蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是多少厘米?(结果保留π)