（人教版）2023-2024学年九年级数学上册 23.1图形...

更新时间：2023-11-07 浏览次数：38 类型：同步测试

一、选择题

1. (2023九上·滕州开学考) 如图，将边长为 $\text{[math]}$ 的正方形 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到正方形 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，那么图中点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九上·深圳月考) 如图，在△ABC中，AB＝AC＝4，∠BAC＝120°，P为BC边上一动点，连接AP，将线段AP绕点A顺时针旋转120°至AP′，则线段PP′的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九上·福田开学考) 如图，平行四边形ABCD中，AB＝16，AD＝12，∠A＝60°，E是边AD上一点，且AE＝8，F是边AB上的一个动点，将线段EF绕点E逆时针旋转60°，得到EG ，连接BG、CG ，则BG+CG的最小值是（）

A . 4 B . 4 $\text{[math]}$ C . 4 $\text{[math]}$ D . 4 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022九上·芜湖期中) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ，连接 $\text{[math]}$ ，将线段 $\text{[math]}$ 绕着点A顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，则线段 $\text{[math]}$ 的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022九上·义乌期中) 如图，正方形ABCD的边长为4， $\text{[math]}$ ，点E是直线CM上一个动点，连接BE，线段BE绕点B顺时针旋转45°得到BF，连接DF，则线段DF长度的最小值等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·温州月考) 如图，二次函数 $\text{[math]}$ 与x轴交于A、B两点，与y轴交于C点，点D与点C关于x轴对称，点P从点A出发向点D运动，点Q在DB上，且∠PCQ＝45°，则图中阴影部分的面积变化情况是（）

A . 一直增大 B . 始终不变 C . 先减小后增大 D . 先增大后减小

答案解析收藏纠错 + 选题
7. (2021九上·三台期中) 如图，已知∠BAC＝60°，AB＝4，AC＝6，点P在△ABC内，将 $\text{[math]}$ APC绕着点A逆时针方向旋转60°得到 $\text{[math]}$ AEF．则AE+PB+PC的最小值为（）

A . 2 $\text{[math]}$ B . 8 C . 5 $\text{[math]}$ D . 6 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021九上·温岭期中) 在平面直角坐标系中，点A（-3，3），B（-4，1），C（-2，1），点M（2，m）绕坐标原点O逆时针旋转90°后，恰好落在△ABC内部（不包括边界），则m的取值范围为（）

A . $\text{[math]}$ <m< $\text{[math]}$ B . $\text{[math]}$ <m< $\text{[math]}$ C . $\text{[math]}$ <m< $\text{[math]}$ D . $\text{[math]}$ <m< $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020九上·慈溪月考) 已知正方形MNOK和正六边形ABCDEF的边长均为1，把正方形放在正六边形中，使OK边与AB边重合，如图所示，按下列步骤操作：将正方形在正六边形中绕点B顺时针旋转，使KM边与BC边重合，完成第一次旋转；再绕点C顺时针旋转，使MN边与CD边重合，完成第二次旋转，……，在这样连续6次旋转的过程中，点B，M之间的距离可能是（）

A . 1.4 B . 1.1 C . 0.8 D . 0.5

答案解析收藏纠错 + 选题
10. (2020九上·深圳期中) 如图4，矩形ABCD绕点A逆时针旋转90*得矩形AEFG，连接CF，交AD于点P，M是CF的中点，连接AM，交EF于点Q。则下列结论：

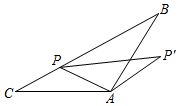
①AM⊥CF；②△CDP≌△AEQ ；③连接PQ，则PQ= $\text{[math]}$ MQ；④若AB=2，BC=6，则MQ= $\text{[math]}$ 其中，正确结论的个数有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

11. (2022九上·南开期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， O为 $\text{[math]}$ 的中点，M为 $\text{[math]}$ 边上一动点，将 $\text{[math]}$ 绕点A逆时针旋转角 $\text{[math]}$ 得到 $\text{[math]}$ ，点M的对应点为 $\text{[math]}$ ，连接 $\text{[math]}$ ，在旋转过程中，线段 $\text{[math]}$ 的长度的最小值是．

答案解析收藏纠错 + 选题
12. (2022九上·普陀期中) 如图，在Rt $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是斜边 $\text{[math]}$ 的中线，将 $\text{[math]}$ 绕点A旋转，点B、C的对应点分别是点E、F，如果点F在射线 $\text{[math]}$ 上，那么 $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题
13. (2021九上·准格尔旗期末) 如图，已知正方形ABCD的边长为6，点E是AB边上一动点，连接ED，将ED绕点E顺时针旋转90°到EF，连接DF，CF，则DF+CF的最小值是．

答案解析收藏纠错 + 选题
14. (2022九上·长沙开学考) 如图，在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 是 $\text{[math]}$ 上一动点，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点， $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ 给出结论： $\text{[math]}$ ； $\text{[math]}$ ；③若正方形的边长为2，则点 $\text{[math]}$ 在射线 $\text{[math]}$ 上运动时， $\text{[math]}$ 有最小值 $\text{[math]}$ 其中结论正确的是．

答案解析收藏纠错 + 选题
15. (2021九上·柯桥月考) 如图，“心”形是由抛物线 $\text{[math]}$ 和它绕着原点O ，顺时针旋转60°的图形经过取舍而成的，其中顶点C的对应点为D ，点A ， B是两条抛物线的两个交点，点E ， F ， G是抛物线与坐标轴的交点，则AB= ．

答案解析收藏纠错 + 选题

三、解答题

16. (2020九上·通河期中) 如图，已知正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF=45°，将△DAE绕点D逆时针旋转90°，得到△DCM．若AE=1，求FM的长．

答案解析收藏纠错 + 选题
17. (2017九上·香坊期末) 如图，在△ABC中，点E在线段AB上，点D在射线CB上，且ED=EC，将△BCE绕点C顺时针旋转60°至△ACF（点B、E的对应点分别为点A、F），连接EF．
1. （1）求证：AE=DB；
2. （2）在不添加任何辅助线的情况下，请直接写出图中四对线段，使每对线段长度之和等于AB的长．
答案解析收藏纠错 + 选题
18. (2023九上·清苑月考)
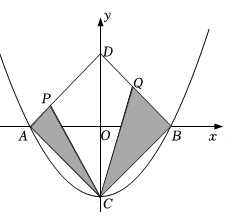
发现：一次小组合作探究课上，嘉嘉将两个正方形按如图1所示的位置摆放（点E ， A ， D在同一条直线上），发现 $\text{[math]}$ 且 $\text{[math]}$ ．
探究：将正方形 $\text{[math]}$ 绕点A按逆时针方向旋转（如图2），还能得到 $\text{[math]}$ 吗?若能，请给出证明；若不能，请说明理由．

答案解析收藏纠错 + 选题
19. (2017九上·江津期末) 如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C＝90°，∠B＝∠E＝30°．
1. （1）操作发现：如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，
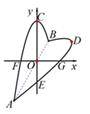
  ①△ADC是三角形；
  ②设△BDC的面积为 $\text{[math]}$ ，△AEC的面积为 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是．
2. （2）猜想论证：当△DEC绕点C旋转到如图3所示的位置时，小明猜想（1）中 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想．
3. （3）拓展探究：如图4，已知∠ABC＝60°，点D是角平分线上一点，且BD＝CD＝4，DE∥AB交BC于点E．若在射线BA上存在点F，使S_△_DCF=S_△_BDE ，请直接写出相应的BF的长．
答案解析收藏纠错 + 选题

四、综合题

20. (2022九上·丰城开学考) 在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点C顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E.
1. （1）当点E恰好在AC上时，如图1，求∠ADE的大小；
2. （2）若α＝60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形.
答案解析收藏纠错 + 选题
21. (2023九上·丛台月考) 如图①所示，将一个边长为2的正方形 $\text{[math]}$ 和一个长为2、宽为1的长方形 $\text{[math]}$ 拼在一起，构成一个大的长方形 $\text{[math]}$ ．现将小长方形 $\text{[math]}$ 绕点C顺时针旋转至长方形 $\text{[math]}$ ，旋转角为 $\text{[math]}$ ．
1. （1）当点 $\text{[math]}$ 恰好落在 $\text{[math]}$ 边上时，求旋转角 $\text{[math]}$ 的值；
2. （2）如图②，G为 $\text{[math]}$ 中点，且 $\text{[math]}$ ，求证： $\text{[math]}$ ；
3. （3）小长方形 $\text{[math]}$ 绕点C顺时针旋转一周的过程中， $\text{[math]}$ 与 $\text{[math]}$ 能否全等？若能，直接写出旋转角 $\text{[math]}$ 的值；若不能，说明理由．
答案解析收藏纠错 + 选题
22. (2022九上·定海期中) 如图，四边形 $\text{[math]}$ 是正方形，连接 $\text{[math]}$ ，将 $\text{[math]}$ 绕点A逆时针旋转α得到 $\text{[math]}$ ，连接 $\text{[math]}$ ， O为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ .
1. （1）如图1，当 $\text{[math]}$ 时，求证： $\text{[math]}$ .
2. （2）如图2，当 $\text{[math]}$ 时，（1）中的结论还成立吗？请说明理由.
答案解析收藏纠错 + 选题
23. (2022九上·南开期中) 将矩形纸片 $\text{[math]}$ 放在平面直角坐标系中，点 $\text{[math]}$ ，点 $\text{[math]}$ ，点 $\text{[math]}$ ．现绕点O顺时针旋转矩形纸片 $\text{[math]}$ ，得到新的矩形 $\text{[math]}$ ，其中A，B，C的对应点分别为 $\text{[math]}$ ．当直线 $\text{[math]}$ 与直线 $\text{[math]}$ 有交点时，设交点为D．
1. （1）在旋转过程中，判断线段 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系，并以图①为例说明理由；
2. （2）在旋转过程中，当点 $\text{[math]}$ 落在线段 $\text{[math]}$ 上时（如图②），直接写出点 $\text{[math]}$ 的坐标；
3. （3）在旋转过程中，若线段 $\text{[math]}$ 恰好过线段 $\text{[math]}$ 中点E时（如图③），求线段 $\text{[math]}$ 的长；
4. （4）在旋转过程中，当线段 $\text{[math]}$ 与线段 $\text{[math]}$ 的交点M恰好是线段 $\text{[math]}$ 中点时（如图④），请直接写出点M和点D的坐标．
答案解析收藏纠错 + 选题