（人教版）2024年中考数学一轮复习图形的性质--命题和证...

更新时间：2023-11-26 浏览次数：48 类型：一轮复习

一、选择题

1. (2023·庆阳模拟) 下面命题正确的是（）

A . 矩形对角线互相垂直
B . 方程 $\text{[math]}$ 的解为 $\text{[math]}$ C . 六边形内角和为 $\text{[math]}$ D . 一对直角三角形，有一组斜边和直角边对应相等，则这两个直角三角形全等

答案解析收藏纠错 + 选题
2. (2023·莲湖模拟) 下列命题：①若 $\text{[math]}$ ，则 $\text{[math]}$ ；②同旁内角互补，两直线平行；③相等的角是对顶角；④无限小数是无理数.其中假命题的是（）

A . ①② B . ②③ C . ②③④ D . ①③④

答案解析收藏纠错 + 选题
3. (2024八下·宝安期中) 命题：已知 $\text{[math]}$ ， $\text{[math]}$ ．求证： $\text{[math]}$ ．运用反证法证明这个命题时，第一步应假设（）成立

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 且 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·南山模拟) 数学知识在生产和生活中被广泛应用，下列实例所应用的最主要的几何知识，说法正确的是（）

A . 射击时，瞄准具的缺口、准星和射击目标在同一直线上，应用了“两点确定一条直线”； B . 车轮做成圆形，应用了“圆是中心对称图形”； C . 学校门口的伸缩门由菱形而不是其他四边形组成，应用了“菱形的对角线互相垂直平分”； D . 地板砖可以做成矩形，应用了“矩形对边相等”．

答案解析收藏纠错 + 选题
5. (2022·鄞州模拟) 能说明命题“对于任意实数 $\text{[math]}$ ， $\text{[math]}$ ”是假命题的反例为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九下·东区月考) 下列说法正确的是（）

A . “清明时节雨纷纷”是必然事件 B . 为了了解一批灯管的使用寿命，可以采用普查的方式进行 C . 一组数据2，5，4，5，6，7的众数、中位数和平均数都是5 D . 甲、乙两组队员身高数据的方差分别为 $\text{[math]}$ ， $\text{[math]}$ ，那么乙组队员的身高比较整齐

答案解析收藏纠错 + 选题
7. (2021八上·宁波期末) 能说明“锐角 $\text{[math]}$ ，锐角 $\text{[math]}$ 的和是锐角”是假命题的例证图是（）.

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2022·海拉尔模拟) 下列命题正确的是（）

A . 圆心角的度数等于圆周角的度数的2倍 B . 有两边相等的平行四边形是菱形 C . 若 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 有最大值2 D . 若 $\text{[math]}$ ，则抛物线 $\text{[math]}$ 与x轴没有交点

答案解析收藏纠错 + 选题
9. (2022·惠山模拟) 下列命题中，是真命题的是（）

A . 长度相等的弧是等弧 B . 如果|a|=1，那么a=1 C . 两直线平行，同位角相等 D . 如果x＞y ，那么－2x＞－2y

答案解析收藏纠错 + 选题
10. (2021·湖里模拟) 用反证法证明命题：“在三角形中，至多有一个内角是直角”，正确的假设是（）

A . 在三角形中，至少有一个内角是直角 B . 在三角形中，至少有两个内角是直角 C . 在三角形中，没有一个内角是直角 D . 在三角形中，至多有两个内角是直角

答案解析收藏纠错 + 选题

二、填空题

11. (2022·西城模拟) 用一个a的值说明命题“若 $\text{[math]}$ ，则 $\text{[math]}$ ”是错误的，这个值可以是 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2024九下·白山模拟) 用一个a的值说明“若a是实数，则2a一定比a大”是错误的，这个值可以是．

答案解析收藏纠错 + 选题
13. (2022·杭州模拟) 能说明命题“若x＞-4，则x²＞16”是假命题的一个反例可以是.

答案解析收藏纠错 + 选题
14. (2024八上·攀枝花开学考) 命题“如果a+b=0，那么a，b互为相反数”的逆命题为.

答案解析收藏纠错 + 选题
15. (2021·泰州模拟) 命题“若 $\text{[math]}$ ，则 $\text{[math]}$ ”是命题.（填“真”或“假”）.

答案解析收藏纠错 + 选题

三、解答题

16. (2022·石城模拟) 已知 $\text{[math]}$ ，且 $\text{[math]}$ ，求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2021·云岩模拟) 同学们，你们知道吗？三角形的内角和不一定是180°.
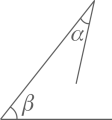
德国数学家黎曼创立的黎曼几何中描述：在球面上选三个点连线构成一个三角形，这个三角形的内角和大于180°.黎曼几何开创了几何学的新领域，近代黎曼几何在广义相对论里有着重要的应用.同样，在俄国数学家罗巴切夫斯基发表的新几何（简称罗氏几何）中，描述了在双曲面里画出的三角形，它的内角和永远小于180°.罗氏几何在天体理论中有着广泛的应用.而我们所学习的欧氏几何中描述“在平面内，三角形的内角和等于180°”是源于古希腊数学家欧几里得编写的《原本》.欧几里得创造的公理化体系影响了世界2000多年，是整个人类文明史上的里程碑.

请你证明：在平面内，三角形的内角和等于180°.要求画出图形，写出已知、求证和证明.

答案解析收藏纠错 + 选题
18. (2022·房山模拟) 下面是小文设计的“过圆外一点作圆的切线”的作图过程．
已知： $\text{[math]}$ 和圆外一点P．
求作：过点P的 $\text{[math]}$ 的切线．
作法：①连接 $\text{[math]}$ ；作 $\text{[math]}$ 的垂直平分线与 $\text{[math]}$ 交于点M；②以 $\text{[math]}$ 半径作 $\text{[math]}$ ，交 $\text{[math]}$ 于点A，B；③作直线 $\text{[math]}$ ；
所以直线 $\text{[math]}$ 为 $\text{[math]}$ 的切线．
请利用尺规作图补全小文的作图过程，并完成下面的证明．
证明：连接 $\text{[math]}$ ．
∵ $\text{[math]}$ 为 $\text{[math]}$ 的直径，
∴ $\text{[math]}$ ▲ = ▲ $\text{[math]}$ （）（填推理的依据）．
∴ $\text{[math]}$
∵ $\text{[math]}$ 为 $\text{[math]}$ 半径，
∴直线 $\text{[math]}$ 为 $\text{[math]}$ 的切线．（）（填推理的依据）．

答案解析收藏纠错 + 选题
19. (2020·呼和浩特模拟) 证明三角形中位线定理：三角形的中位线平行于第三边，且等于第三边的一半（要求：自己作图并写出已知、求证、证明）

答案解析收藏纠错 + 选题

四、综合题

20. (2022·海陵模拟) 已知：如图，AB是⊙O的直径，AC是⊙O的弦，过点C的直线交AB延长线于点D，给出下列信息：
①∠A＝30°；
②CD是⊙O的切线；
③OB＝BD．
1. （1）请在上述3条信息中选择其中两条作为条件，剩下的一条作为结论．你选择的条件是 ▲ ，结论是 ▲ （只要填写序号）．判断结论是否正确，并说明理由；
2. （2）在（1）的条件下，若CD＝3 $\text{[math]}$ ，求 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题
21. (2022·北京模拟) 已知：如图，直线l ，和直线外一点P ．
求作：过点P作直线PC ，使得PC∥l ，

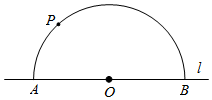
作法：①在直线l上取点O ，以点O为圆心，OP长为半径画圆，交直线l于A ， B两点；

②连接AP ，以点B为圆心，AP长为半径画弧，交半圆于点C；

③作直线PC ．

直线PC即为所求作．
1. （1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
2. （2）完成下面的证明：
  证明：连接BP ．
  
  ∵BC＝AP ，
  
  ∴ $\text{[math]}$ ▲ ．
  
  ∴∠ABP＝∠BPC（）（填推理依据）．
  
  ∴直线PC∥直线l ．
答案解析收藏纠错 + 选题
22. (2022九下·杭州期中) 如图，在△ABC中，点D，E分别在AB，AC上.
1. （1）若BD=CE，CD=BE，求证AB=AC；
2. （2）分别将“BD=CE”记为①，“CD=BE”记为②，“AB=AC”记为③.以①、③为条件，②为结论构成命题1，以②、③为条件，①为结论构成命题2.则命题1是命题，命题2是命题(选择“真”或“假“填入空格)
答案解析收藏纠错 + 选题
23. (2022·六盘水) 为倡导“全民健身，健康向上”的生活方式，我市教育系统特举办教职工气排球比赛．比赛采取小组循环，每场比赛实行三局两胜制，取实力最强的两支队伍参加决赛，从C组的比分胜负表中知道二中胜4场负1场．
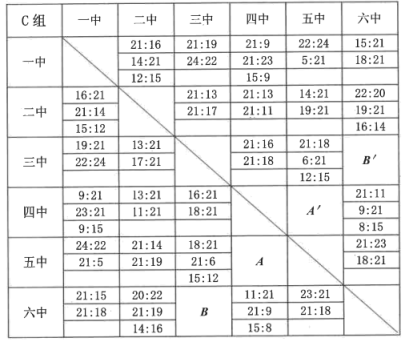
教职工气排球比赛比分胜负表
1. （1）根据表中数据可知，一中共获胜场，“四中VS五中”的比赛获胜可能性最大的是；
2. （2）若 $\text{[math]}$ 处的比分是21∶10和21∶8，并且参加决赛的队伍是二中和五中，则 $\text{[math]}$ 处的比分可以是和；（两局结束比赛，根据自己的理解填写比分）；
3. （3）若 $\text{[math]}$ 处的比分是10∶21和8∶21， $\text{[math]}$ 处的比分是21∶18，15∶21，15∶12，那么实力最强的是哪两支队伍，请说明理由．
答案解析收藏纠错 + 选题