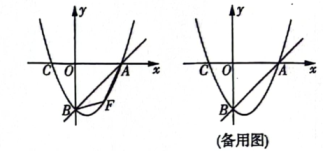
B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 


图1 图2
每件售价x(元) | … | 15 | 16 | 17 | 18 | … |
每天销售量y(件) | … | 150 | 140 | 130 | 120 | … |

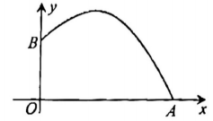
①求L的解析式:
②求点P到AB距离的最大值.
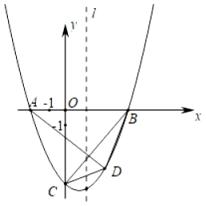
①当A、B两点纵坐标相等时,求AB中点的坐标。
②设图象G的最高点的纵坐标与最低点的纵坐标的差为h,求h与a的函数关系式,并写出a的取值范围.
①求(用含
的代数式表示);
②求与
之间的函数关系式,并求出
的最小值.