

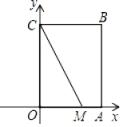


方法1:
方法2:

关于勾股定理的研究有一个很重要的内容是勾股数组,在数学课本中我们已经了解到,“能够成为直角三角形三条边的三个正整数称为勾股数”,以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法:
方法1:若m为奇数(m≥3),则a=m,b= (m2﹣1)和c=
(m2+1)是勾股数.
方法2:若任取两个正整数m和n(m>n),则a=m2﹣n2 , b=2mn,c=m2+n2是勾股数.
三角形中至少有一边长为10 cm;三角形中至少有一边上的高为8 cm,
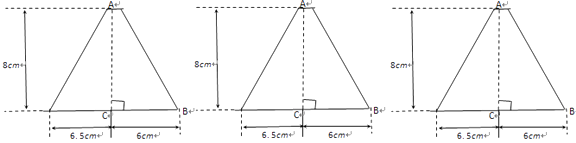
请设计出三种面积不同的方案并在图上画出分割线,求出相应图形面积.