①三角形的内角和等于180°; ②如果|x|=5,那么x=5; ③1月份有30天; ④作一条线段等于已知线段; ⑤一个锐角与一个钝角互补吗?



“有一个角为30°且有一条直角边为2的直角三角形是平方三角形”是 命题;(填“真”或“假”)
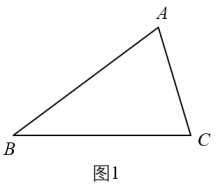
①如图1,若 ,
,
,求
的值.
②如图2,若 ,求优比
的取值范围.
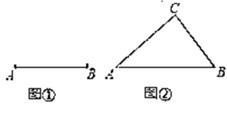
①判断,命题:“如果直角三角形是奇异三角形,那么奇异中线一定是较长直角边上的中线”是真命题还是假命题;
②请用直尺和圆规在图①中画一个以AB为边的“奇异三角形“;