备考2024年中考数学探究性训练专题9 二元一次方程（组）

更新时间：2024-03-24 浏览次数：25 类型：二轮复习

一、选择题

1. 在“幻方拓展课程”探索中，小明在如图的3×3方格内填入了一些表示数的代数式，若图中各行、各列及对角线上的三个数之和都相等，则x-y=（）

A . 2 B . 4 C . 6 D . 8

答案解析收藏纠错 + 选题
2. (2023九上·文成开学考) 如图是小慧用列表法研究关于x，y的二元一次方程 $\text{[math]}$ 整数解的规律，如图是小慧列表的部分内容.由表可知m，n的值分别为（）

x

-1

0

1

2

5

y

-7

-3

1

m

n

A . 3，9 B . 3，17 C . 5，9 D . 5，17

答案解析收藏纠错 + 选题
3. (2023七下·嵊州期末) “九宫图”传说是远古时代洛河中的一个神龟背上的图案，故又称“龟背图”，中国古代数学史上经常研究这一神话．数学上的“九宫图”所体现的是一个 $\text{[math]}$ 表格，每一行的三个数，每列的三个数，斜对角的三个数之和都相等，也称为三阶幻方，如图是一个满足条件的三阶幻方的一部分，则 $\text{[math]}$ 的值为（）

4

3

$\text{[math]}$
-1

$\text{[math]}$

A . 9 B . $\text{[math]}$ C . 36 D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021七下·西山期末) 我国古代很早就对二元一次方程组进行研究，其中不少成果被收入古代数学著作《九章算术》．《九章算术》中的“方程”一章中讲述了算筹图，如图1．图2所示，图中各行从左到右列出的算筹数分别表示未知数xy的系数与相应的常数项．图1表示的算筹图用我们现在所熟悉的方程组形式表述出来为 $\text{[math]}$ 类似地，图2所示的算筹图我们可以表述为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024七上·长兴期末) 小明和小亮在一起探究一个数学活动.首先小亮站立在箱子上，小明站立在地面上（如图1），然后交换位置（如图2），测量的数据如图所示，想要探究的问题有：①小明的身高；②小亮的身高；③箱子的高度；④小明与小亮的身高和.根据图上信息，你认为可以计算出的是（）

A . ① B . ② C . ③ D . ④

答案解析收藏纠错 + 选题

二、填空题

6. (2023八上·南宁月考) 三个同学对问题“若方程组 $\text{[math]}$ 的解是 $\text{[math]}$ ，求方程组 $\text{[math]}$ 的解”提出各自的想法．甲说：“这个题目条件不够，不能求解”；乙说：“它们的系数有一定规律，可以试试”；丙说“能不能把第二个方程组的两个方程的两边都除以 $\text{[math]}$ ，通过换元替代的方法来解决” $\text{[math]}$ 参考他们的讨论，求出方程组的解是．

答案解析收藏纠错 + 选题
7. (2020七下·沙河口期末) 我国古代很早就开始对一次方程组进行研究，很多题目保留至今，如《九章算术》中有这样的一道古代问题，“有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛，1个大桶加上5个小桶可以盛酒2斛.1个大桶、1个小桶分别可以盛酒多少斛？”在这个问题中，如果设1个大桶可以盛酒 $\text{[math]}$ 斛，1个小桶可以盛酒 $\text{[math]}$ 斛，根据题意，可列方程组为.”

答案解析收藏纠错 + 选题

三、理论探究题

8. (2023七下·铁锋期中) 综合与探究：
如图，在平面直角坐标系中，有 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点，其中 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 满足关系式 $\text{[math]}$ ．
1. （1）求A、B、 $\text{[math]}$ 三点的坐标；
2. （2）如果在第二象限内有一点 $\text{[math]}$ ，请用含 $\text{[math]}$ 的式子表示四边形 $\text{[math]}$ 的面积；
3. （3）在（2）的条件下，当 $\text{[math]}$ 时，在 $\text{[math]}$ 轴上是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ 的面积等于四边形 $\text{[math]}$ 的面积的2倍？若存在，请直接写出点 $\text{[math]}$ 的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
9. (2023七下·北仑期末) 数学活动：探究不定方程
小北，小仑两位同学在学习方程过程中，发现三元一次方程组 $\text{[math]}$ ，虽然解不出x，y，z的具体数值，但可以解出 $\text{[math]}$ 的值．
1. （1）小北的方法： $\text{[math]}$ ，整理可得： $\text{[math]}$ ；
  $\text{[math]}$ ，整理可得： $\text{[math]}$ ，∴ $\text{[math]}$ ．
  小仑的方法： $\text{[math]}$ ：③；∴得： $\text{[math]}$ ．
2. （2）已知 $\text{[math]}$ ，试求解 $\text{[math]}$ 的值．
3. （3）学校现准备采购若干英语簿，数学簿以及作文本，已知采购4本英语簿，5本数学簿，2本作文本需要6元；采购4本英语簿，8本数学簿，2本作文本需要7.2元，那么采购200本英语簿，300本数学簿，100本作文本需要多少钱？
答案解析收藏纠错 + 选题
10. (2023七下·沭阳期中) 阅读下面的材料：若 $\text{[math]}$ ，求m，n的值．
解： $\text{[math]}$ $\text{[math]}$ ．

$\text{[math]}$ $\text{[math]}$

$\text{[math]}$ $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ ．

$\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ．

$\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ．

根据你的观察，探究下列问题：
1. （1）若 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
3. （3）已知 $\text{[math]}$ 的三边长a，b，c都是正整数，且满足 $\text{[math]}$ ，求 $\text{[math]}$ 的周长．
答案解析收藏纠错 + 选题
11. (2022七下·江都期末) 某数学实验小组在探究“关于x的二次三项式ax²+bx+3的性质（a、b为常数）”时，进行了如下活动．
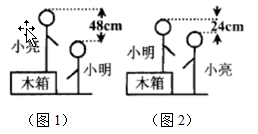
【实验操作】取不同的x的值，计算代数式ax²+bx+3的值．
x
…
﹣1
0
1
2
3
…
ax²+bx+3
…
0
3
4
…
1. （1）根据上表，计算出a、b的值，并补充完整表格．
2. （2）【观察猜想】实验小组组员，观察表格，提出以下猜想．同学甲说：“代数式ax²+bx+3的值随着x的增大而增大”．同学乙说：“不论x取何值，代数式ax²+bx+3的值一定不大于4”．
  请你也提出一个合理的猜想：
3. （3）【验证猜想】我们知道，猜想有可能是正确的，也可能是错误的．
  请你分别判断甲、乙两位同学的猜想是否正确，若不正确，请举出反例；若正确，请加以说理．
答案解析收藏纠错 + 选题
12. (2019七下·南浔期末) 你知道数学中的整体思想吗?解题中，若把注意力和着眼点放在问题的整体上，多方位思考、联想、探究，进行整体思考、整体加减，能使问题迅速获解.
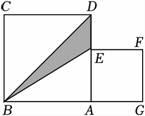
例题：已知x²+xy=4，xy+y²=-1.求代数式x²-y²的值.

解：将两式相减，得(x²+xy)-(xy+y²)=4-(-1)，即x²-y²=5；请用整体思想解答下列问题：
1. （1）在例题的基础上求(x+y)²的值；
2. （2）若关于x、y的二元一次方程组 $\text{[math]}$ 的解也是二元一次方程x+y=6的解，求k的值.
答案解析收藏纠错 + 选题
13. 对于任意实数a，b，定义新运算“⊗”：a⊗b=2a+b.例如：3⊗4=2×3+4=10.
1. （1）求2⊗(-5)的值.
2. （2）若x⊗(-y)=2，且2y⊗x=-1，求x+y的值.
答案解析收藏纠错 + 选题
14. 在解方程组 $\text{[math]}$ 时，明明采用了一种“整体代换”的解法.
解：将方程②变形为4x+10y+y=5，即2(2x+5y)+y=5.③
把①代入③，得2×3+y=5，解得y=-1.
把y=-1代入①，得x=4，
∴方程组的解决为 $\text{[math]}$
请用“整体代换”法解下列方程组：
1. （1） $\text{[math]}$ 。
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
15. 善于思考的小明在解方程组 $\text{[math]}$ 时，采用了一种“整体代换”的思想，解法如下：
解：将方程8x+22y=10变形为2（4x+10y）+2y=10.③
把方程①代入③，得2×6+2y=10，解得 y=-1.
把y=-1代入①，得x=4，
∴原方程组的解为 $\text{[math]}$
请你运用“整体代换”的思想解决下列问题：
1. （1）解方程组 $\text{[math]}$
2. （2）已知x，y，z满足 $\text{[math]}$ 试求 z 的值.
答案解析收藏纠错 + 选题
16. 对于实数x，y，定义新运算“*”： $\text{[math]}$ .其中a，b是常数，等式右边是通常的加法和乘法运算，已知1*2=1，（-3）*3=6.求：
1. （1） a，b的值.
2. （2） 2*（-4）的值.
答案解析收藏纠错 + 选题
17. ⑴[阅读理解] 对于方程组 $\text{[math]}$ ，不妨设 $\text{[math]}$ =a， $\text{[math]}$ =b，则原方程组就转化成以a，b为未知数的方程组 $\text{[math]}$ ，解得 $\text{[math]}$ ．从而求得原方程组的解是 $\text{[math]}$ ，这种解法称之为换元法．
⑵[问题解决] 用换元法解方程组： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2023八上·期中) 我们用[a]表示不大于a的最大整数，例如：[2.5]＝2，[3]＝3，[-2.5]＝-3；用＜a＞表示大于a的最小整数，例如：＜2.5＞＝3，＜3＞＝4，＜-2.5＞＝-2．根据上述规定，解决下列问题：
1. （1） [-4.5]＝，＜3.01＞＝；
2. （2）若x为整数，且[x]+＜x＞＝2023，求x的值；
3. （3）若x、y满足方程组 $\text{[math]}$ ，求x、y的取值范围．
答案解析收藏纠错 + 选题
19. (2022八上·鄞州期中) 阅读以下材料：对于三个数a ， b ， c ，用M{a ， b ， c}表示这三个数的平均数，用min{a、b ， c}表示这三个数中最小的数．例如：M{﹣1，2，3}＝ $\text{[math]}$ ， min{-1，2，3}＝﹣1；min{﹣1，2，a}＝ $\text{[math]}$ 解决下列问题：
1. （1） min{ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ }＝，若min{2，2x+2，4﹣2x}＝2，则x的范围为；
2. （2） ①如果M{2，x+1，2x}＝min{2，x+1，2x}，求x；
  ②根据①，你发现了结论“如果M{a ， b ， c}＝min{a ， b ， c}，那么（填a ， b ， c的大小关系）”．证明你发现的结论；
  ③运用②的结论，填空：若M{2x+y+2，x+2y ， 2x﹣y}＝min{2x+y+2，x+2y，2x﹣y}，则x+y＝．
答案解析收藏纠错 + 选题

四、数形结合探究题

20. (2024八上·前郭尔罗斯期末) 在理解例题的基础上，完成下列两个问题：
例题：若 $\text{[math]}$ ，求m和n的值；
解：由题意得： $\text{[math]}$ ，
∴ $\text{[math]}$ ∴ $\text{[math]}$ ，解得 $\text{[math]}$ ．
请解决以下问题：
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
2. （2）若a，b，c是 $\text{[math]}$ 的边长，满足 $\text{[math]}$ ， c是 $\text{[math]}$ 的最长边，且c为奇数，则c可能取何值？
答案解析收藏纠错 + 选题
21. (2023八上·长春期中) 将完全平方公式（a±b）²＝a²±2ab+b进行适当的变形，可以解决很多的数学问题，例如：若a+b＝3，ab＝1，求a²+b²的值．
解：因为a+b＝3，所以（a+b）²＝9，即a²+2ab+b²＝9．
又因为ab＝1，所以a²+b²＝7．
根据上面的解题思路与方法，解决下列问题：
1. （1）若x+y＝8，x²+y²＝40，则xy＝；
2. （2）若x﹣y＝6，xy＝5，求x²+y²的值；
3. （3）两个正方形ABCD、AEFG如图摆放，面积和为34，BG＝8，则图中阴影部分面积为．
答案解析收藏纠错 + 选题
22. (2023八上·盐湖月考) 综合与实践
小许是个爱动脑筋的学生，她在学习了二元一次方程组后遇到了这样一道题目：如图1，长方形 $\text{[math]}$ 中放置 $\text{[math]}$ 个形状和大小都相同的小长方形（尺寸如图 $\text{[math]}$ ），求图中阴影部分的面积．
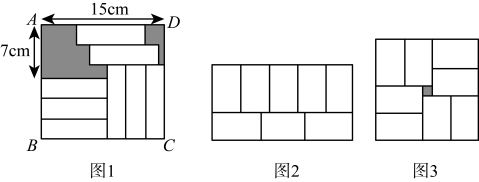
1. （1）小许设小长方形的长为 $\text{[math]}$ ，宽为 $\text{[math]}$ ，观察图形得出关于 $\text{[math]}$ ， $\text{[math]}$ 的二元一次方程组，解出 $\text{[math]}$ ， $\text{[math]}$ 的值，再用大长方形的面积减去 $\text{[math]}$ 个小长方形的面积得到阴影部分的面积．
2. （2）解决问题：
  请按照小许的思路完成上述问题：
  动手实践：解决完上面的问题后，小许在家里找了 $\text{[math]}$ 张形状大小都相同的卡片，恰好拼成了一个大的长方形如图 $\text{[math]}$ 所示，打乱后又拼成如图 $\text{[math]}$ 那样的大正方形，中间还留了一个洞，恰好是边长为 $\text{[math]}$ 的小正方形，求每个小长方形的面积．请给出解答过程．
答案解析收藏纠错 + 选题

五、实践探究题

23. (2023·温州模拟) 根据以下素材，探索完成任务.

如何设计奖品购买及兑换方案？
素材1	某文具店销售某种钢笔与笔记本，已知钢笔的单价是笔记本的2倍，用120元购买笔记本的数量比用160元购买钢笔的数量多8件.
素材2	某学校花费400元购买该文具店的钢笔和笔记本作为奖品颁发给“优秀学生”，两种奖品的购买数量均不少于20件，且购买笔记本的数量是10的倍数.
素材3	学校花费400元后，文具店赠送m张 $\text{[math]}$ 兑换券（如右）用于商品兑换.兑换后，笔记本与钢笔数量相同.
问题解决
任务1	探求商品单价	请运用适当方法，求出钢笔与笔记本的单价.
任务2	探究购买方案	探究购买钢笔和笔记本数量的所有方案.
任务3	确定兑换方式	运用数学知识，确定一种符合条件的兑换方式.

答案解析收藏纠错 + 选题

24.
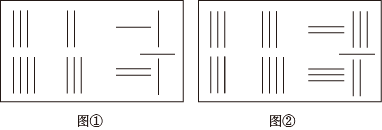
现实生活中，镶嵌图案在地面、墙面乃至于服装面料设计中随处可见．在八年级课题学习“平面图形的镶嵌”中，对于单种多边形的镶嵌，主要研究了三角形、四边形、正六边形的镶嵌问题．今天我们把正多边形的镶嵌作为研究问题的切入点，提出其中几个问题，共同来探究.
我们知道，可以单独用正三角形、正方形或正六边形镶嵌平面．如图，用正方形镶嵌平面，可以发现在一个顶点O周围围绕着4个正方形的内角.

试想：如果用正六边形镶嵌平面，在一个顶点周围应该围绕个正六边形内角．
问题提出
如果我们要同时用两种不同的正多边形镶嵌平面，可能设计出几种不同的组合方案？
问题解决
猜想1：是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌？
分析：我们可以将此问题转化为数学问题来解决．从平面图形的镶嵌中可以发现，解决问题的关键在于分析能同时用于完整镶嵌平面的两种正多边形的内角特点．具体地说，就是在镶嵌平面时，一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角．
验证1：在镶嵌平面时，设围绕某一点有x个正方形和y个正八边形的内角可以拼成一个周角．根据题意，可得方程：
$\text{[math]}$ ，整理得： $\text{[math]}$ ，
我们可以找到惟一一组适合方程的正整数解为 $\text{[math]}$ ．
结论1：镶嵌平面时，在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角，所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌．
猜想2：是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌？若能，请按照上述方法进行验证，并写出所有可能的方案；若不能，请说明理由．
上面，我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况，仅仅得到了一部分组合方案，相信同学们用同样的方法，一定会找到其它可能的组合方案．
问题拓广
请你仿照上面的研究方式，探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案，并写出验证过程．

答案解析收藏纠错 + 选题
25. (2021七下·建华期末) 综合与探究
列方程组解应用问题要先审题、找相等关系，再设未知数、列方程，最后解方程、写出答案．设未知数时可采用“直接设法”与“间接设法”．
甲、乙两名同学在做下面应用题：“嫩江是齐齐哈尔的母亲河，为加强河坝的防洪能力，现有一段长为180米的河坝加固任务由 $\text{[math]}$ 、 $\text{[math]}$ 两个工程队先后接力完成． $\text{[math]}$ 工程队每天加固河道12米， $\text{[math]}$ 工程队每天加固河道8米，共用时20天．求 $\text{[math]}$ 、 $\text{[math]}$ 两工程队分别加固河道多少米？”请你根据所给题目，解决下列问题：
1. （1）如果甲同学采用直接设法：
  可设 $\text{[math]}$ 表示                  ▲                   ， $\text{[math]}$ 表示                  ▲                   ，
  那么依题意可列方程组：（ $\text{[math]}$    ），解得（ $\text{[math]}$    ）
  如果乙同学采用间接设法：
  可设 $\text{[math]}$ 表示                  ▲                   ， $\text{[math]}$ 表示                  ▲                   ，
  那么依题意可列方程组：（ $\text{[math]}$          ），解得（ $\text{[math]}$          ）
2. （2）请你直接写出 $\text{[math]}$ 、 $\text{[math]}$ 两工程队分别加固河道多少米？
答案解析收藏纠错 + 选题

26. (2024七下·桂林月考) 根据以下信息，探索完成任务：

如何设计招聘方案？
素材 $\text{[math]}$	某汽车制造厂开发一款新式电动汽车，计划一年生产安装 $\text{[math]}$ 辆 $\text{[math]}$ 每名熟练工均能独立安装电动汽车，由于抽调不出足够的熟练工来完成新式电动汽车的安装，工厂决定招聘一些新工人，经过培训上岗可以独立进行安装．
素材 $\text{[math]}$	调研部门发现： $\text{[math]}$ 名熟练工和 $\text{[math]}$ 名新工人每月可安装 $\text{[math]}$ 辆电动汽车； $\text{[math]}$ 名熟练工和 $\text{[math]}$ 名新工人每月可安装 $\text{[math]}$ 辆电动汽车．
素材 $\text{[math]}$	工厂给安装电动汽车的每名熟练工每月发 $\text{[math]}$ 元工资，每名新工人每月发 $\text{[math]}$ 元工资．

（1）【任务一分析数量关系】每名熟练工和新工人每月分别可以安装多少辆电动汽车？
（2）【任务二：确定可行方案】如果工厂招聘 $\text{[math]}$ 名新工人，使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务，那么工厂有哪几种工人的招聘方案？
（3）【任务三：选取最优方案】在上述方案中，为了节省成本，应该招聘新工人名 $\text{[math]}$ 直接写出答案 $\text{[math]}$

答案解析收藏纠错 + 选题

27. (2024八上·浙江期末) 根据以下素材，探索完成任务．

探究奖项设置和奖品采购的方案

素材1

如图，某学校举办“迎亚运庆国庆”知识竞赛，分别设置一等奖、二等奖和三等奖的奖品．已知一盒水笔比一本笔记本的单价多10元，6盒水笔和3本笔记本的总价为150元．

素材2

若设置的获奖总人数不变，为提高同学们的参赛积极性，学校计划对获奖级别及人数进行调整，如下表：

（1）【探求商品单价】请运用适当方法，求出每盒水笔和每本笔记本的价格．
（2）【探究设奖方案】求m，n所有可能的
（3）【选择最优方案】选择去哪家超市购买比较合算，请说明理由

答案解析收藏纠错 + 选题

28. 阅读材料：

某市地铁公司规定：普通成人持储值卡乘坐地铁出行，每个自然月内，达到规定消费累计金额后的乘次，享受相应的折扣优惠（如图）.地铁出行消费累计金额月底清零，次月重新累计.

每个自然月内﹐普通成人持储值卡乘坐地铁：

消费累计金额≤150元，九五折；

150元≤消费累计金额≤200元，九折；

200元≤消费累计金额≤300元，八折；

消费累计金额≥>300元，七五折.

例如：李老师2月无储值卡消费 260元，若采用新规持储值卡消费，则需付费 150×0.95+50×0.9+60×0.8=235.5（元）.

解决问题：

甲、乙两个成人2月无储值卡乘坐地铁的消费金额合计300元（甲消费金额超过150元，但不超过200元）.若两人采用新规持储值卡消费，则共需付费283.5元.问甲、乙2月无储值卡乘坐地铁的消费金额各是多少元？

答案解析收藏纠错 + 选题

29.

如何利用闲置纸板箱制作储物盒
素材 1	如图1是小琴家需要设置储物盒的区域，该区域可以近似看成一个长方体，底面尺寸如图2所示.
素材 2	如图3、图4是利用闲置纸板箱拆解出的①，②两种一边均为a(cm)(a<50)的矩形纸板.
	纸板①(单位：cm)			纸板②(单位：cm)

	小琴分别将纸板①和②以不同的方式制作储物盒.
	纸板①的制作方式			纸板②的制作方式
	裁去角上4个相同的小正方形，折成一个无盖长方体储物盒.			将纸片四个角裁去4个相同的小矩形，折成一个有盖的长方体储物盒。
目标 1	熟悉材料			⑴若按照纸板①的制作方式制成的储物盒恰好完全放入储物区域，则长方形纸板的宽a= cm.
目标 2		利用目标1计算所得的数据a，进行进一步探究.
		初步应用	⑵按照纸板①的制作方式，为了更方便地放入或取出储物盒，盒子四周需要留出一定的空间，当储物盒的底面积是936cm²时，求储物盒的容积.
		储物收纳	⑶按照纸板②的制作方式制作储物盒，EF和HG两边恰好重合且无重叠部分，盒子的底面积为702cm².家里一个玩具机械狗的尺寸如图所示，请通过计算判断该机械狗能否完全放入储物盒.

答案解析收藏纠错 + 选题

30. 小聪想用现有的硬纸板裁成如图1所示的长方形和正方形作为侧面与底面，做成如图2所示的竖式和横式两种无盖纸盒.已知一张硬纸板的裁剪方式有两种(均有余料)：方式一：裁成3个长方形与一个正方形；方式二：裁成2个长方形与2个正方形.小聪将m张硬纸板按方式一裁剪，n张硬纸板按方式二裁剪.
1. （1）两种方式共裁出长方形张，正方形张(均用含m，n的代数式表示).
2. （2）当10<m<15时，若所裁得的长方形与正方形纸板恰好用完，所做盒子一样多，则做成的两种无盖纸盒一共可能是多少个
答案解析收藏纠错 + 选题

31. (2023八上·浙江月考) 根据以下素材，探索完成任务.

探究奖项设置和奖品采购的方案

素材1

如图，某学校举办“迎亚运庆国庆”知识竞赛，分别设置一等奖、二等奖和三等奖的奖品.已知一盒水笔比一本笔记本的单价多10元，6盒水笔和3本笔记本的总价为150元.

素材2

若设置的获奖总人数不变，为提高同学们的参赛积极性，学校计划对获奖级别及人数进行调整，如下表：

获奖级别	一等奖	二等奖	三等奖
调整前人数（单位：个）	5	15	30
调整后人数（单位：个）	m	20	n

注：调整后增加一等奖人数，且学校购买奖品的预算经费控制在2050元之内.

素材3

调整后开始采购，了解到A，B两家超市均在搞促销活动.A超市买4盒水笔送1本笔记本，B超市所有商品九折出售.

问题解决

任务1

探求商品单价

请运用适当方法，求出每盒水笔和每本笔记本的价格.

任务2

探究设奖方案

求m，n所有可能的值.

任务3

选择最优方案

选择去哪家超市购买比较合算，请说明理由.

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

备考2024年中考数学探究性训练专题9 二元一次方程（组）

副标题：

*注意事项：

备考2024年中考数学探究性训练专题9 二元一次方程（组）

试题分析

总体分析

题量分析

难度分析

知识点分析

x	…	﹣1	0	1	2	3	…
ax²+bx+3	…	0	3	4			…