备考2024年中考数学探究性训练专题18 相交线与平行线

更新时间：2024-03-31 浏览次数：66 类型：二轮复习

一、选择题

1. (2023七下·遵义月考) 小红在“趣味数学”社团活动中探究了直线交点个数的问题．现有7条不同的直线ln(n=1，2，3，4，5，6，7)，其中l₁、l₂互相平行，l₃、l₄、I₅三条直线交于一点，则他探究这7条直线的交点个数最多是（）

A . 17个 B . 18个 C . 19个 D . 21个

答案解析收藏纠错 + 选题
2. (2022七下·绵阳期末) 在探究“过直线外一点P作已知直线a的平行线”的活动中，王玲同学通过如下的折纸方式找到了符合要求的直线，在这个过程中她可能用到的推理依据组合是（）

①平角的定义；②邻补角的定义；③角平分线的定义；④同旁内角互补，两直线平行；⑤两直线平行，内错角相等．

A . ②④ B . ③⑤ C . ①②⑤ D . ①③④

答案解析收藏纠错 + 选题
3. (2022八上·科尔沁期末) 在探究证明“三角形的内角和是180°”时，综合实践小组的同学作了如下四种辅助线，其中不能证明“三角形内角和是180°”的是（）

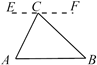A . 过C作EF $\text{[math]}$ AB B . 过AB上一点D作DE 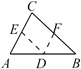$\text{[math]}$ BC，DF $\text{[math]}$ AC C . 延长AC到F，过C作CE $\text{[math]}$ AB D . 作CD⊥AB于点D

答案解析收藏纠错 + 选题
4. (2020八上·孝南月考) 加强对课本习题的探究，对解题有很好的指导作用.如课本第82页有这样一题，如图，AD//BC，BD平分∠ABC，求证：AB=AD.
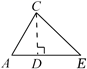
可将这个题目归纳为：平行加角平分线，得到等腰三角形.请利用这个结论解题：如图，已知△ABC中，I是∠A，∠B，∠C的平分线的交点，AB=6，BC=5，AC=4.平移∠A，使点A与点I重合，两边分别交BC于D，E两点，则△IDE的周长为（）

A . 4 B . 5 C . 6 D . 9

答案解析收藏纠错 + 选题

二、填空题

5. (2022七下·花都期末) 在数学活动课上，老师让同学们以“两块直角三角板（一块含 $\text{[math]}$ 角，一块含 $\text{[math]}$ 角）的摆放”为背景开展数学探究活动．某同学将两块三角板按如图所示放置，则下列结论正确的有（直接写序号即可）．
① $\text{[math]}$ ；②若 $\text{[math]}$ ，则 $\text{[math]}$ ；③若 $\text{[math]}$ ，则 $\text{[math]}$ ；④若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
6. (2021七下·乾安期中) 探究规律：我们有可以直接应用的结论：若两条直线平行，那么在一条直线上任取一点，无论这点在直线的什么位置，这点到另一条直线的距离均相等．例如：如图1，两直线 $\text{[math]}$ ，两点 $\text{[math]}$ 、 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ，则 $\text{[math]}$ ．
如图2，已知直线 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 为直线 $\text{[math]}$ 上的两点， $\text{[math]}$ 、 $\text{[math]}$ 为直线 $\text{[math]}$ 上的两点．
1. （1）请写出图中面积相等的各对三角形：．
2. （2）如果 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为三个定点，点 $\text{[math]}$ 在 $\text{[math]}$ 上移动，那么无论 $\text{[math]}$ 点移动到任何位置总有：与 $\text{[math]}$ 的面积相等；理由是：．
答案解析收藏纠错 + 选题
7. (2020九下·石家庄开学考) 观察下面图形，按要求找角（不含平角），如图①，两条直线交于同一点O，共有对对顶角；如图②，三条直线交于同一点O，共有对对顶角；探究：若有 $\text{[math]}$ 条直线相交于同一点，则可形成对对顶角．

答案解析收藏纠错 + 选题
8. (2021·安徽模拟) 在数学探究活动中，“创新”小组进行了如下操作：如图，将矩形纸片ABCD的一角沿过点C的直线折叠，使得点B落在边AD的点H处，再将另一角沿过点C的直线折叠，使得点D落在CH的点Q处，两次折叠的折痕分别为CE、CF。请完成以下探究：
1. （1） ∠BEC+∠DFC的大小为；
2. （2）若AB=3，BC=5时， $\text{[math]}$ 的值为。
答案解析收藏纠错 + 选题
9. (2020·硚口模拟) （问题探究）如图1， $\text{[math]}$ ，直线 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离为2，点 $\text{[math]}$ 到 $\text{[math]}$ 的距离为1， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的最小值是；（提示：将线段 $\text{[math]}$ 沿 $\text{[math]}$ 方向平移1个单位长度即可解决，如图2所示.）
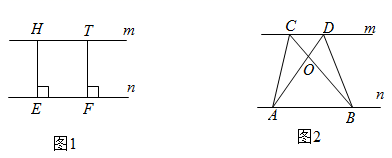
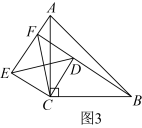
（关联运用）如图3，在等腰 $\text{[math]}$ 和等腰 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 在直线 $\text{[math]}$ 上， $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值是.

答案解析收藏纠错 + 选题

三、作图题

10. (2021七上·西城期末) 小冬阅读了教材中“借助三角尺画角”的探究活动（如图1、图2的实物图所示），他在老师指导下画出了图1所对应的几何图形，并标注了所使用三角尺的相应角度（如图3），他发现用一副三角尺还能画出其他特殊角．
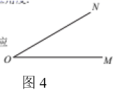
请你借助三角尺完成以下画图，并标注所使用三角尺的相应角度．
1. （1）画出图2对应的几何图形；
2. （2）设计用一副三角尺画出 $\text{[math]}$ 角的画图方案，并画出相应的几何图形；
3. （3）如图4，已知 $\text{[math]}$ ，画∠MON的角平分线OP．
答案解析收藏纠错 + 选题

四、实践探究题

11. (2019九下·锡山月考) 感知：如图①，在四边形ABCD中，AB∥CD，∠B=90°，点P在BC边上，当∠APD=90°时，可知△ABP∽△PCD．（不要求证明）
探究：如图②，在四边形ABCD中，点P在BC边上，当∠B=∠C=∠APD时，求证：△ABP∽△PCD．

拓展：如图③，在△ABC中，点P是边BC的中点，点D、E分别在边AB、AC上．若∠B=∠C=∠DPE=45°，BC=6 $\text{[math]}$ ，CE=4，求DE的长

答案解析收藏纠错 + 选题
12. (2023七下·五华期末) 小明在一组平行线中作角，探究两边与平行线形成的锐角的数量关系．
1. （1）如图1，他先作出 $\text{[math]}$ ，且点 $\text{[math]}$ 在一条直线上，当 $\text{[math]}$ 时， $\text{[math]}$ ．点 $\text{[math]}$ 在两条平行线之间，如图2，请用等式表示 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系并证明．
2. （2）在图3中， $\text{[math]}$ ，点 $\text{[math]}$ 在两条平行线之间，记 $\text{[math]}$ 与图中一条直线形成的锐角为 $\text{[math]}$ ，若小明作射线 $\text{[math]}$ ，使得 $\text{[math]}$ ，记 $\text{[math]}$ 与图中另一条直线形成的锐角为 $\text{[math]}$ ，请用等式表示 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系．
答案解析收藏纠错 + 选题
13. (2020八上·阳泉期末) 综合与探究

【问题】如图1，在Rt△ABC中，∠ACB=90°，AC=BC，过点C作直线l平行于AB，∠EDF=90，点D在直线l上移动，角的一边DE始终经过点B，另一边DF与AC交于点P，研究DP和DB的数量关系。

【探究发现】
1. （1）如图2，某数学学习小组运用“从特殊到一般”的数学思想，发现当点D移动到使点P与点C重合时，很容易就可以得到DP=DB，请写出证明过程；
2. （2）如图3，若点P是AC上的任意一点(不含端点A、C)，受(1)的启发，另一个学习小组过点D作DG⊥CD交BC于点G，就可以证明DP=DB，请完成证明过程。
3. （3）若点P是CA延长线上的任意一点，在图(4)中补充完整图形，并判断结论是否仍然成立。
答案解析收藏纠错 + 选题
14. (2023七下·番禺期末) 如图，已知格线相互平行，小明在格线中作∠AOB、∠CPD、∠EOF，探究角的两边与格线形成的锐角所满足的数量关系.
1. （1）如图1，∠AOB=60°，点O在一条格线上，当∠1=20°时，求∠2的度数；
2. （2）如图2，∠CPD=60°，点Р在两条格线之间，用等式表示∠3与∠4的数量关系，并证明；
3. （3）如图3，∠EOF=60°，小明在图3中作射线QG，使得∠GOF=45°.记QG与图中一条格线形成的锐角为α，QE与图中另一条格线形成的锐角为β，探究α与β的数量关系，并用等式表示α与β的数量关系.
答案解析收藏纠错 + 选题
15. (2023七下·忻州期末) 综合与探究
1. （1）如图1， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系为；如图2， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系为．
2. （2）在图3中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
3. （3）在图4中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，试探究 $\text{[math]}$ 、 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系．
答案解析收藏纠错 + 选题
16. (2023七下·梅江期末) 直线在同一平面内有平行和相交两种位置关系，线段首尾连接可以变换出很多不同的图形，这些不同的角又有很多不同关系，今天我们就来探究一下这些奇妙的图形吧！
【问题探究】
1. （1） ①如图1，若 $\text{[math]}$ ，点P在 $\text{[math]}$ 内部， $\text{[math]}$ ，则 $\text{[math]}$ ；
  ②如图2，若 $\text{[math]}$ ，将点P在 $\text{[math]}$ 外部，求 $\text{[math]}$ 之间数量关系（不需证明）；
  ③如图3，写出 $\text{[math]}$ 之间的数量关系：（不需证明）．
2. （2）如图4，五角星 $\text{[math]}$ ，请直接写出 $\text{[math]}$ ．
3. （3）如图5，将五角星 $\text{[math]}$ 去掉一个角后， $\text{[math]}$ 是多少？请证明你的结论．
答案解析收藏纠错 + 选题
17. 在学习了图形的旋转知识后，某数学兴趣小组对教材中有关图形旋转的问题进行了进一步探究.
1. （1）问题梳理：
  问题呈现：如图1，点D在等边三角形ABC的边BC上，过点C作AB的平行线l，在l上取CE=BD，连结AE，则在图1中会产生一对旋转图形.请结合问题中的条件，证明：△ABD≌△ACE.
2. （2）初步尝试：
  如图2，在△ABC中，AB=AC，点D在边BC上，且BD<DC，将△ABD沿某条直线翻折，使得AB与AC重合，点D与BC边上的点F重合，再将△ACF沿AC所在直线翻折，得到△ACE，则在图2中会产生一对旋转图形.若∠BAC=30°，AD=6，连结DE，求△ADE的面积.
3. （3）深入探究：
  如图3，在△ABC中， $\text{[math]}$ AC=6，D是边BC上的任意一点，连结AD，将线段AD绕点A按逆时针方向旋转75°，得到线段AE，连结CE，求线段CE长度的最小值.
答案解析收藏纠错 + 选题
18. (2023七下·南山期中)

【问题提出】小颖同学在学习中自主探究以下问题，请你解答她提出的问题：
1. （1）如图 $\text{[math]}$ 所示，已知 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ ， $\text{[math]}$ 之间一点，连接 $\text{[math]}$ ， $\text{[math]}$ ，得到 $\text{[math]}$ 请猜想 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系，并证明；
  猜想： ▲ ；
  证明：
2. （2）如图 $\text{[math]}$ 所示，已知 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ ， $\text{[math]}$ 之间一点， $\text{[math]}$ 和 $\text{[math]}$ 的平分线相交于点 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
3. （3）【类比迁移】小颖结合角平分线的知识将问题进行深入探究，如图 $\text{[math]}$ 所示，已知： $\text{[math]}$ ，点 $\text{[math]}$ 的位置移到 $\text{[math]}$ 上方，点 $\text{[math]}$ 在 $\text{[math]}$ 延长线上，且 $\text{[math]}$ 平分 $\text{[math]}$ 与 $\text{[math]}$ 的平分线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，请直接写出 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系；
4. （4）【变式挑战】小颖在本次探究的最后将条件 $\text{[math]}$ 去掉，提出了以下问题：
  已知 $\text{[math]}$ 与 $\text{[math]}$ 不平行，如图 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上，点 $\text{[math]}$ 在 $\text{[math]}$ 上，连接 $\text{[math]}$ ，且 $\text{[math]}$ 同时平分 $\text{[math]}$ 和 $\text{[math]}$ ，请直接写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系．
答案解析收藏纠错 + 选题
19. 小明完成作业后在家复习，他看到七下课本第12页例4，感到这个结论十分有趣，便尝试探究起来.
1. （1）【基础巩固】
  与例4条件和结论互换，改成了：“如图1，AP 平分∠BAC，CP平分∠ACD，AB∥CD，则∠1+∠2=90°，”小明认为这个结论正确，你赞同他的想法吗? 请说明理由.
2. （2）【尝试探究】
  小明发现：若将其中一条角平分线改成AC的垂线，则“∠1+∠2=90°”这个结论不成立.请帮小明完成探究：
  如图2，AB∥CD，AP平分∠BAC，CP⊥AC，∠1是AP与AB的夹角，∠2 是CP与CD的夹角.
  ①若∠2=22°，求∠1的度数.
  ②试说明：2∠1-∠2=90°.
3. （3）【拓展提高】
  如图3，若AB∥CD，AP⊥AC，CP平分∠ACD，请直接写出∠1与∠2的数量关系.
答案解析收藏纠错 + 选题
20. (2024七下·修水期中) 综合与探究
数学活动课上，老师以“一个含 $\text{[math]}$ 的直角三角板和两条平行线”为背景展开探究活动，
如图1，已知直线 $\text{[math]}$ ，直角三角板 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）如图1，若 $\text{[math]}$ ，则 $\text{[math]}$ ；（直接写出答案）
2. （2） “启航”小组在图1的基础上继续展开探究：如图 $\text{[math]}$ ，调整三角板的位置，当三角板 $\text{[math]}$ 的直角顶点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，直线 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 相交时，他们得出的结论是： $\text{[math]}$ ，你认为启航小组的结论是否正确，请说明理由；
3. （3）如图 $\text{[math]}$ ，受到“启航”小组的启发，“睿智”小组提出的问题是：在图 $\text{[math]}$ 的基础上，继续调整三角板的位置，当点 $\text{[math]}$ 不在直线 $\text{[math]}$ 上，直线 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 相交时， $\text{[math]}$ 与 $\text{[math]}$ 有怎样的数量关系？请你用平行线的知识说明理由．
答案解析收藏纠错 + 选题
21. (2024九上·深圳期末) 某数学学习小组学习完四边形后进行了如下探究，已知四边形 $\text{[math]}$ 为矩形，请你帮助他们解决下列问题：
1. （1）【初步尝试】：他们将矩形 $\text{[math]}$ 的顶点E、G分别在如图（1）所示的 $\text{[math]}$ 的边 $\text{[math]}$ 、 $\text{[math]}$ 上，顶点F、H恰好落在 $\text{[math]}$ 的对角线 $\text{[math]}$ 上，求证： $\text{[math]}$ ：
2. （2）【深入探究】：如图2，若 $\text{[math]}$ 为菱形， $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
3. （3）【拓展延伸】：如图（3），若 $\text{[math]}$ 为矩形， $\text{[math]}$ ； $\text{[math]}$ 且 $\text{[math]}$ ，请直接写出此时 $\text{[math]}$ 的值是（用含有m ， n的代数式表示）.
答案解析收藏纠错 + 选题
22. (2023八上·义乌开学考) 数学兴趣小组围绕“三角形的内角和是 $\text{[math]}$ ”，进行了一系列探究，过程如下：
1. （1）【论证】如图 $\text{[math]}$ ，延长 $\text{[math]}$ 至点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，就可以说明 $\text{[math]}$ 成立，即：三角形的内角和为 $\text{[math]}$ 请完成上述说理过程．
2. （2）【应用】如图 $\text{[math]}$ ，在 $\text{[math]}$ 中， $\text{[math]}$ 的平分线与 $\text{[math]}$ 的角平分线交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ， $\text{[math]}$ 在射线 $\text{[math]}$ 上，且 $\text{[math]}$ ， $\text{[math]}$ 的延长线与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ．
  $\text{[math]}$ 求 $\text{[math]}$ 的度数；
  $\text{[math]}$ 设 $\text{[math]}$ ，请用 $\text{[math]}$ 的代数式表示 $\text{[math]}$ ．
3. （3）【拓展】如图 $\text{[math]}$ ，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，直线 $\text{[math]}$ 与 $\text{[math]}$ 相交于 $\text{[math]}$ 点右侧的点 $\text{[math]}$ ， $\text{[math]}$ 绕点 $\text{[math]}$ 以每秒 $\text{[math]}$ 的速度顺时针方向旋转，同时 $\text{[math]}$ 绕点 $\text{[math]}$ 以每秒 $\text{[math]}$ 的速度顺时针方向旋转，与 $\text{[math]}$ 重合时 $\text{[math]}$ 再绕着点 $\text{[math]}$ 以原速度逆时针方向旋转，当 $\text{[math]}$ 旋转一周时，运动全部停止 $\text{[math]}$ 设运动时间为 $\text{[math]}$ 秒，在旋转过程中，是否某一时刻，使得 $\text{[math]}$ 与 $\text{[math]}$ 的一边平行？若存在，求 $\text{[math]}$ 的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
23. (2023八上·新丰期中) 综合探究
如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的平分线， $\text{[math]}$ 是 $\text{[math]}$ 边上的高，垂足为 $\text{[math]}$ ，设 $\text{[math]}$ ．
1. （1）探究与发现
  ① 如图1，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为 ▲ ， $\text{[math]}$ 的度数为 ▲ ；
  ② 如图2，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为 ▲ ；
  ③ 试探究 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由．
2. （2）拓展与思考
  如图3， $\text{[math]}$ 的平分线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．当 $\text{[math]}$ 时，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
24. (2024九上·锦江期末) 某托管服务数学兴趣小组针对如下问题进行探究，在等边 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在射线 $\text{[math]}$ 上运动，连接 $\text{[math]}$ ，以 $\text{[math]}$ 为一边在 $\text{[math]}$ 右侧作等边 $\text{[math]}$ ．
1. （1）【问题发现】如图 $\text{[math]}$ ，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上运动时 $\text{[math]}$ 不与点 $\text{[math]}$ 重合 $\text{[math]}$ ，连接 $\text{[math]}$ 则线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是；直线 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系是；
2. （2）【拓展延伸】如图 $\text{[math]}$ ，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上运动时，直线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ，请探究 $\text{[math]}$ 的面积与 $\text{[math]}$ 的面积之间的数量关系；
3. （3）【问题解决】当点 $\text{[math]}$ 在射线 $\text{[math]}$ 上运动时 $\text{[math]}$ 点 $\text{[math]}$ 不与点 $\text{[math]}$ ， $\text{[math]}$ 重合 $\text{[math]}$ ，直线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ，若 $\text{[math]}$ 的面积是 $\text{[math]}$ ，请求出线段 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
25. (2023七下·子洲期末) 【问题背景】
如图， $\text{[math]}$ ．连接 $\text{[math]}$ ，点E，F在 $\text{[math]}$ 上，且 $\text{[math]}$ ，连接 $\text{[math]}$ ，且 $\text{[math]}$ ．

【问题探究】
1. （1）试说明： $\text{[math]}$ ：
2. （2）若 $\text{[math]}$ ，
  ①试判断 $\text{[math]}$ 的形状，并说明理由：
  
  ②若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
26. (2022八上·宝应期中) 某校一数学兴趣小组在一次合作探究活动中，将两块大小不同的等腰直角三角形 $\text{[math]}$ 和等腰直角三角形 $\text{[math]}$ ，按如图1的方式摆放， $\text{[math]}$ ．该数学兴趣小组进行如下探究，请你帮忙解答：
1. （1）【初步探究】如图1，试探究 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系，并说明理由；
2. （2）【深入探究】如图2，当 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点共线时，请探究此位置时线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系，并说明理由；
3. （3）【拓展延伸】如图3，当 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点不共线时，连接 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，请猜想此位置时线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系：．
答案解析收藏纠错 + 选题
27. (2023七下·新都期末) 学习完平行线的知识后，甲，乙，丙三位同学利用两个三角形进行探究活动，分别得到以下图形．已知 $\text{[math]}$ 中， $\text{[math]}$ ．请根据他们的叙述条件完成题目．
1. （1）若 $\text{[math]}$ 为等腰直角三角形，且 $\text{[math]}$ ；
  ①甲同学：如图1， $\text{[math]}$ 和 $\text{[math]}$ 的直角边 $\text{[math]}$ 在同一直线上，点E和点C互相重合，斜边 $\text{[math]}$ 与 $\text{[math]}$ 相交于点P，那么∠APF= ▲ 度；
  
  ②乙同学：如图2， $\text{[math]}$ 和 $\text{[math]}$ 直角顶点C，D互相重合于点P，斜边 $\text{[math]}$ 与斜边 $\text{[math]}$ 互相平行，求 $\text{[math]}$ 的度数，并写出解答过程；
2. （2）若 $\text{[math]}$ 为等腰三角形，已知 $\text{[math]}$ ．
  丙同学：如图3，若 $\text{[math]}$ 直角顶点D恰好与 $\text{[math]}$ 底边 $\text{[math]}$ 的中点重合， $\text{[math]}$ 的斜边 $\text{[math]}$ 经过 $\text{[math]}$ 的顶点C，若 $\text{[math]}$ ，设 $\text{[math]}$ ，请用含x的式子表示 $\text{[math]}$ 的度数，并写出解答过程．
答案解析收藏纠错 + 选题
28. (2023七下·承德期末) 问题情境：在数学探究活动课上，老师让同学们以“两条平行线 $\text{[math]}$ ， $\text{[math]}$ 和一块含30°角的直角三角板 $\text{[math]}$ ”为主题开展数学探究活动．
1. （1）探究发现：如图-1，小明把三角板 $\text{[math]}$ 的60°角的顶点 $\text{[math]}$ 放在 $\text{[math]}$ 上，若 $\text{[math]}$ ，则 $\text{[math]}$ °；
2. （2）如图-2，小亮把三角板 $\text{[math]}$ 的两个锐角的顶点 $\text{[math]}$ ， $\text{[math]}$ 分别放在 $\text{[math]}$ 和 $\text{[math]}$ 上，请你探索并说明 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系；
3. （3）如图-3，小颖把三角板 $\text{[math]}$ 的直角顶点 $\text{[math]}$ 放在 $\text{[math]}$ 上，30°角的顶点 $\text{[math]}$ 放在 $\text{[math]}$ 上．若 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的度数（用含 $\text{[math]}$ 的代数式表示）；
4. （4）拓展延伸：若将如图-3所示的三角形 $\text{[math]}$ 绕直角顶点 $\text{[math]}$ 顺时针旋转一周，每秒转动10°，直接写出当 $\text{[math]}$ 时，三角形 $\text{[math]}$ 旋转所用的时间 $\text{[math]}$ （用含 $\text{[math]}$ 的代数式表示）．
答案解析收藏纠错 + 选题
29. (2023七下·海曙期中) 数学探究活动中，阿青同学为了验证：长条纸片上下边沿 $\text{[math]}$ 与 $\text{[math]}$ 是否平行，把纸片沿着 $\text{[math]}$ 折叠（如图1），并用量角器测出 $\text{[math]}$ 的度数；
1. （1）若 $\text{[math]}$ ，则 $\text{[math]}$ .你认为阿青同学的做法正确吗？㳻说明理由；
2. （2）在（1）的条件下，阿青同学在纸条下 $\text{[math]}$ 上取点 $\text{[math]}$ （如图2），连结 $\text{[math]}$ 并沿着 $\text{[math]}$ 折叠纸片使得 $\text{[math]}$ 与 $\text{[math]}$ 重合，过 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，设 $\text{[math]}$ ， $\text{[math]}$ .
  ①当点 $\text{[math]}$ 在点 $\text{[math]}$ 之间时，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
  ②当点 $\text{[math]}$ 在 $\text{[math]}$ 上的运动过程中， $\text{[math]}$ 和 $\text{[math]}$ 之间有怎样的数量关系？请写出你的猜想，并加以证明.（选其中一种情况证明）
答案解析收藏纠错 + 选题