

有以下结论:
①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ
②当∠PAQ=30°,PQ=9时,可得到形状唯一确定的△PAQ
③当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ
④当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ

其中所有正确结论的序号是( )

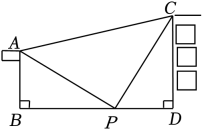
如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE , 其中结论正确的个数为( )

如图,在正n边形(n为整数,且n≥4)绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为正n边形的“叠弦角”,△AOP为“叠弦三角形”.以下说法,正确的是.(填番号)
①在图1中,△AOB≌△AOD';
②在图2中,正五边形的“叠弦角”的度数为360°;
③“叠弦三角形”不一定都是等边三角形; ④正n边形的“叠弦角”的度数为60°﹣ .


【阅读理解题】初二(1)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
(Ⅰ)如图1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,延长BC至E,使 ,
, 最后测出DE的距离即为AB的长;
(Ⅱ)如图2,先过B点作AB的垂线BF,再在BF上取C、D两点使 , 接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.

阅读后回答下列问题:

