2023-2024学年广东省深圳市七年级下学期数学期中仿真模...

更新时间：2024-04-14 浏览次数：177 类型：期中考试

一、选择题（本大题共10小题，每小题3分，共30分，每小题有四个选项，只有一个是正确的）

1. (2023七下·宝安期末) $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023七下·南山期中) 蚕丝是大自然中的天然纤维，是中国古代文明产物之一，也成为散发着现代科学技术魅力的新材料 $\text{[math]}$ 某蚕丝的直径大约是 $\text{[math]}$ 米， $\text{[math]}$ 用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023七下·南山期中) 下面四个图形中， $\text{[math]}$ 一定成立的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024七下·南海期中) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022七上·哈尔滨月考) 下列图形中，由 $\text{[math]}$ ，能得到 $\text{[math]}$ 的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2024七下·桑植期中) 下列各式中，不能用平方差公式计算的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. 若 $\text{[math]}$ 是完全平方式，则 p的值为（）

A . 1 B . ±2 C . ±1 D . ±4

答案解析收藏纠错 + 选题
8. (2023七下·东莞期中) 如图，直线 $\text{[math]}$ ， $\text{[math]}$ 被直线 $\text{[math]}$ 所截， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023七下·龙岗期末) 【观察】① $\text{[math]}$ ；
② $\text{[math]}$ ；

③ $\text{[math]}$ ；

……

【归纳】由此可得： $\text{[math]}$ ；

【应用】请运用上面的结论，计算： $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023七下·岳池期中) 如图，已知，∠BAC=∠ACD=90°，∠ABC=∠ADC，CE⊥AD．有下列结论：①AD∥BC；②∠ECD=∠DAC；③∠CEF=∠CFE；④CACE=∠ABC．其中正确的结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（本题有5小题，每小题3分，共15分）

11. (2023七下·光明期中) 老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如下： $\text{[math]}$ ，则所指的多项式为．

答案解析收藏纠错 + 选题
12. (2021七下·普宁期中) 若一个角的补角比这个角的余角的3倍大10°，则这个角为度．

答案解析收藏纠错 + 选题
13. (2023七下·宝安期中) 已知8•（2^m）ⁿ＝64，|n|＝1，则m＝．

答案解析收藏纠错 + 选题
14. (2023七下·深圳期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 的角平分线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2023七下·顺德期中) 如图是某灯具的镜面反射示意图，从光源点 $\text{[math]}$ 处发出的光线 $\text{[math]}$ ， $\text{[math]}$ 经弯曲的镜面反射后射出，且满足反射光线 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题

三、解答题(本题共7小题，共55分)

16. (2022七下·电白期中) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．（要求用公式简便计算）
答案解析收藏纠错 + 选题
17. (2016七下·河源期中) 化简求值：
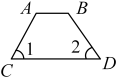
[（x+2y）²﹣（x﹣2y）²﹣（x+2y）（x﹣2y）﹣4y²]÷2x，其中x=﹣2，y= $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2023七下·紫金期中) 已知：∠ $\text{[math]}$ ．请你用直尺和圆规画一个∠BAC，使∠BAC=∠ $\text{[math]}$ ．（要求：要保留作图痕迹．）

答案解析收藏纠错 + 选题
19. (2023七下·禅城期中) 填空并完成以下证明：
已知，如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ，求证： $\text{[math]}$ ．

证明： $\text{[math]}$ 已知 $\text{[math]}$

$\text{[math]}$                      ．

$\text{[math]}$ 已知 $\text{[math]}$

$\text{[math]}$ （）

$\text{[math]}$                       .（）

$\text{[math]}$ 已知 $\text{[math]}$

$\text{[math]}$                         .（）

$\text{[math]}$ （）

$\text{[math]}$                     $\text{[math]}$ .（）

$\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2024七下·新宁月考) 如图，是由四个长为 $\text{[math]}$ ，宽为 $\text{[math]}$ 的小长方形拼成的正方形．
1. （1）图中的阴影正方形的边长可表示为 $\text{[math]}$ 用含 $\text{[math]}$ ， $\text{[math]}$ 的代数式表示 $\text{[math]}$ ；
2. （2）根据图形中的数量关系，请你结合图形直接写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的一个等量关系；
3. （3）根据(2)中的结论，解决下列问题：若 $\text{[math]}$ ， $\text{[math]}$ ，求阴影正方形的面积．
答案解析收藏纠错 + 选题
21. (2023七下·盐田期末) 佳佳和萌萌一起参加中长跑，起跑后路程 $\text{[math]}$ 与时间 $\text{[math]}$ 之间的关系如图所示．
1. （1）在上述关系中，自变量是，因变量是；
2. （2）这次比赛的路程是m；
3. （3）萌萌将本次中长跑分起跑、途中跑和冲刺跑三阶段，经历了两次变速，在第 $\text{[math]}$ 速度最慢，速度为 $\text{[math]}$ ；
4. （4）通过计算说明萌萌与佳佳何时相遇．
答案解析收藏纠错 + 选题
22. (2023七下·深圳期中) 【概念认识】
两条直线相交所形成的锐角或直角称为这两条直线的夹角，如果两条直线的夹角为α，那么我们称这两条直线是“α相交线”例如；如图①，直线m和直线n为“α相交线”我们已经知道两条平行线被第三条直线所截，同位角相等、内错角相等、同旁内角互补，那么若两条直线为“α相交线”，它们被第三条直线所截后形成的同位角、内错角、同旁内角之间有什么关系呢？
1. （1）【初步研究】
  如图②，直线m与直线n是“α相交线”，求证： $\text{[math]}$
  小明的证法如图③．若直线m与直线n交于点O，
  直线m与直线n是“α相交线”．
  ∵ $\text{[math]}$ ．
  ∴ $\text{[math]}$ 是 $\text{[math]}$ 的外角，
  ∴ $\text{[math]}$ ．
  即 $\text{[math]}$ ．
  请补充完整小明的证明过程，并用另一种不同的方法进行证明
2. （2）【深入思考】
  如图④，直线m与直线n是α相交线，
  ①找出直线m与直线n被直线l所截得的内错角，并直接写出内错角与α的关系；
  ②找出直线m与直线n被直线l所截得的同旁内角，并直接写出每对同旁内角与α的关系；
3. （3）【综合运用】
  如图⑤，已知∠α，用直尺和圆规按下列要求作图，
  如图⑥，直线 $\text{[math]}$ 外求作一点M，使得直线 $\text{[math]}$ 与直线 $\text{[math]}$ 是“α相交线”（不写作图过程，保留作图痕迹）．
答案解析收藏纠错 + 选题