
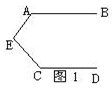





已知:如图1, ,
为
,
之间的点,连接
,
得到
.
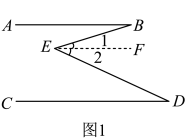
求证: .
证明:如图1,过点作
, ∴
.
∵ ,
, ∴ ▲ .
∴ .
∵ , ∴
.
[问题解答]
①如图2, ,
, 求
的度数;

②如图3, , 分别交
的两边于点
,
,
,
, 点
在射线
上,
,
, 那么当点
在
,
两点之间移动时,
与
,
之间有何数量关系?请说明理由.


请你参考小敏同学的方法,解决下面问题:
背景材料:如图①,若 , 则
理由:过作
, 因为
, 所以,
(如果两条直线都与第三条直线平行,那么这两条直线也互相平行)
由 , 得
, 由
, 得
. (两直线平行,内错角相等)
由 , 所以,
, (等量代换).

如图2,创新小组的同学把直线a向上平移,并把的位置改变,发现
, 请说明理由;
缜密小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,平分
, 此时发现
与
又存在新的数量关系,请直接写出
与
的数量关系.

①当点P在线段上运动时,试探究
,
,
之间的数量关系.
②当点P在线段C,D两点外侧运动时(点P与点C,D,O三点不重合),直接写出 ,
,
之间的数量关系为 .
解:由于点P是平行线之间有一动点,因此需要对点P的位置进行分类讨论:
如图1,当P点在的左侧时,
满足数量关系为,
如图2,当P点在的右侧时,
满足数量关系为.
①若 , 则
.
②猜想与
的数量关系,并说明理由;
③如图4,若与
的角平分线交于点
,
与
的角平分线交于点
,
与
的角平分线交于点
;此次类推,则
与
满足怎样的数量关系?(直接写出结果)


【阅读理解】:两条平行线间的拐点问题经常可以通过作一条直线的平行线进行转化.
例如:如图1, , 点
、
分别在直线
、
上,点
在直线
、
之间.问
,
,
之间有何数量关系?请说明理由.
小铭同学发现 , 并给出了部分理由.
如图 , 过点
作
,
因为 ,
,
所以 ,
…;
如图3, , 点
在
的上方,问
,
,
之间有何数量关系?请说明理由;
如图4,已知 ,
的平分线和
的平分线交于点
, 请你用含有
的式子表示
的度数,直接写出结果.
在“相交线与平行线”的学习中,有这样一道典型问题:
如图①,AB∥CD,点P在AB与CD之间,可得结论:∠BAP+∠APC+∠PCD=360°.

理由如下:
过点P作PQ∥AB.
∴∠BAP+∠APQ=180°.
∵AB∥CD,
∴PQ∥CD.
∴∠PCD+∠CPQ=180°.
∴∠BAP+∠APC+∠PCD
=∠BAP+∠APQ+∠CPQ+∠PCD
=180°+180°
=360°.

【问题解决】
【问题情境】
在一次综合与实践课上,老师让同学们以平行线为主题,进行相关问题的探究,进一步感受平行线在寻找角之间的关系的作用,以下是智慧小组的活动过程,请你加入他们小组一起完成探究.
如图, , 当
,
时,试求∠2的大小;

经过探究发现,图1中的∠1,∠2,∠3之间存在着一定的数量关系,下列选项中能正确表示这种关系的是____;
如图,一条公路经过三次拐弯后又回到原来的方向,若第一次的拐角第三次的拐角
, 则第二次的拐角
.


已知:如图1, , E为
、
之间一点,连接
,
得到
.
探索、
、
之间的数量关系,并说明你的理由.

过点E作 ,
∴
∵ ,
,
∴ ,
……
请接着他的思路完成解答过程.
①如图3,当点B在点A的左侧时,若 ,
, 求
的度数;
②如图4,当点B在点A的右侧时,设 ,
, 直接写出
的度数为 ▲ (用含有
,
的式子表示).
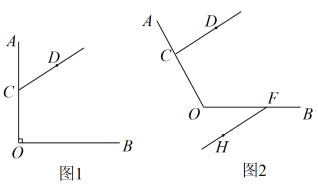
①依据题意,补全图1;
②直接写出∠BOE的度数.
