2024年北师大版数学中考仿真模拟试题（五）

更新时间：2024-04-19 浏览次数：39 类型：中考模拟

一、选择题（每题4分，共40分）

1. (2024·江门模拟) 河湟剪纸被列入青海省第三批省级非物质文化遗产名录，是青海劳动人民结合河湟文化，创造出独具高原特色的剪纸.以下剪纸图案既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023·盘锦) 下列事件中，是必然事件的是（）

A . 任意画一个三角形，其内角和是 $\text{[math]}$ B . 任意买一张电影票，座位号是单号 C . 掷一次骰子，向上一面的点数是3 D . 射击运动员射击一次，命中靶心

答案解析收藏纠错 + 选题
3. (2024八下·锡山月考) 用配方法解一元二次方程 $\text{[math]}$ ，配方后得到的方程是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·镇江) 如图，桌面上有3张卡片，1张正面朝上．任意将其中1张卡片正反面对调一次后，这3张卡片中出现2张正面朝上的概率是（）．

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022九上·交城期末) 在下列四幅图形中，能表示两棵小树在同一时刻阳光下影子的图形的可能是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2023九上·郑州经济技术开发月考) 如图，坡角为α的斜坡上有一棵垂直于水平地面的大树AB，当太阳光线与水平线成45°角沿斜坡照下，在斜坡上的树影BC长为m，则大树AB的高为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. 如图，等圆 $\text{[math]}$ 和 $\text{[math]}$ 相交于A ， B两点， $\text{[math]}$ 经过 $\text{[math]}$ 的圆心 $\text{[math]}$ ，若 $\text{[math]}$ ，则图中阴影部分的面积为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023·张家界) 如图，矩形 $\text{[math]}$ 的顶点A，C分别在y轴、x轴的正半轴上，点D在 $\text{[math]}$ 上，且 $\text{[math]}$ ，反比例函数 $\text{[math]}$ 的图象经过点D及矩形 $\text{[math]}$ 的对称中心M，连接 $\text{[math]}$ ．若 $\text{[math]}$ 的面积为3，则k的值为（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
9. (2023·绵阳) 如图，在边长为4的正方形ABCD中，点G是BC上的一点，且BG＝3GC，DE⊥AG于点E，BF∥DE，且交AG于点F，则tan∠EDF的值为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023·随州) 如图，已知开口向下的抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ ，对称轴为直线 $\text{[math]}$ ．则下列结论正确的有（）
① $\text{[math]}$ ；

② $\text{[math]}$ ；

③方程 $\text{[math]}$ 的两个根为 $\text{[math]}$ ；

④抛物线上有两点 $\text{[math]}$ 和 $\text{[math]}$ ，若 $\text{[math]}$ 且 $\text{[math]}$ ，则 $\text{[math]}$ ．

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（每题4分，共24分）

11. (2023·阜新) 将一个三角尺 $\text{[math]}$ 按如图所示的位置摆放，直线 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是．

答案解析收藏纠错 + 选题
12. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ．以点 $\text{[math]}$ 为圆心，以 $\text{[math]}$ 的长为半径作弧交边 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．分别以点 $\text{[math]}$ 为圆心，以大于 $\text{[math]}$ 的长为半径作弧，两弧交于点 $\text{[math]}$ ，作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交边 $\text{[math]}$ 于点 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
13. (2023·长春) $\text{[math]}$ 年5月8日， $\text{[math]}$ 商业首航完成——中国民商业运营国产大飞机正式起步． $\text{[math]}$ 时 $\text{[math]}$ 分航班抵达北京首都机场，穿过隆重的“水门礼”（寓意“接风洗尘”、是国际民航中高级别的礼仪）．如图①，在一次“水门礼”的预演中，两辆消防车面向飞机喷射水柱，喷射的两条水柱近似看作形状相同的抛物线的一部分．如图②，当两辆消防车喷水口A、B的水平距离为 $\text{[math]}$ 米时，两条水柱在物线的顶点H处相遇，此时相遇点H距地面 $\text{[math]}$ 米，喷水口A、B距地面均为4米．若两辆消防车同时后退 $\text{[math]}$ 米，两条水柱的形状及喷水口 $\text{[math]}$ 、 $\text{[math]}$ 到地面的距离均保持不变，则此时两条水柱相遇点 $\text{[math]}$ 距地面米．

答案解析收藏纠错 + 选题
14. (2024九下·金山模拟) 若关于x的一元一次不等式组 $\text{[math]}$ ，至少有2个整数解，且关于y的分式方程 $\text{[math]}$ 有非负整数解，则所有满足条件的整数a的值之和是．

答案解析收藏纠错 + 选题
15. (2023·海南) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点E在边 $\text{[math]}$ 上，且 $\text{[math]}$ ，点P为边 $\text{[math]}$ 上的动点，连接 $\text{[math]}$ ，过点E作 $\text{[math]}$ ，交射线 $\text{[math]}$ 于点F ，则 $\text{[math]}$ ．若点M是线段 $\text{[math]}$ 的中点，则当点P从点A运动到点B时，点M运动的路径长为．

答案解析收藏纠错 + 选题
16. (2024·南山模拟) 如图，在直角坐标系中， $\text{[math]}$ 与 $\text{[math]}$ 轴相切于点 $\text{[math]}$ 为 $\text{[math]}$ 的直径，点 $\text{[math]}$ 在函数 $\text{[math]}$ 的图象上， $\text{[math]}$ 为 $\text{[math]}$ 轴上一点， $\text{[math]}$ 的面积为6，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

三、解答题（共10题，共86分）

17. (2016·黔东南) 计算：（ $\text{[math]}$ ）^﹣²+（π﹣3.14）⁰﹣| $\text{[math]}$ |﹣2cos30°．

答案解析收藏纠错 + 选题
18. (2023·烟台) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ 是使不等式 $\text{[math]}$ 成立的正整数．

答案解析收藏纠错 + 选题
19. (2023九上·高州期末) 教室里的投影仪投影时，可以把投影光线CA，CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC， $\text{[math]}$ ．黑板上投影图像的高度 $\text{[math]}$ ， CB与AB的夹角 $\text{[math]}$ ，求AC的长．（结果精确到1cm．参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
20. (2017·金华)
如图，在平面直角坐标系中，△ABC各顶点的坐标分别为A(−2，−2)，B(−4，−1），C(−4，−4)．
1. （1）作出 $\text{[math]}$ ABC关于原点O成中心对称的 $\text{[math]}$ A₁B₁C₁.
2. （2）作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 $\text{[math]}$ A₁B₁C₁的内部（不包括顶点和边界），求a的取值范围.
答案解析收藏纠错 + 选题
21. (2023九上·宝安月考) 随着科技的进步，购物支付方式日益增多．为了解某社区居民支付的常用方式（A微信，B支付宝，C现金，D其他），某学习小组对红星社区部分居民进行问卷调查，根据查结果，绘制成如图统计图．
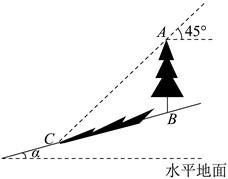
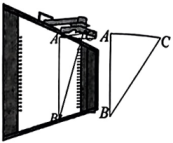
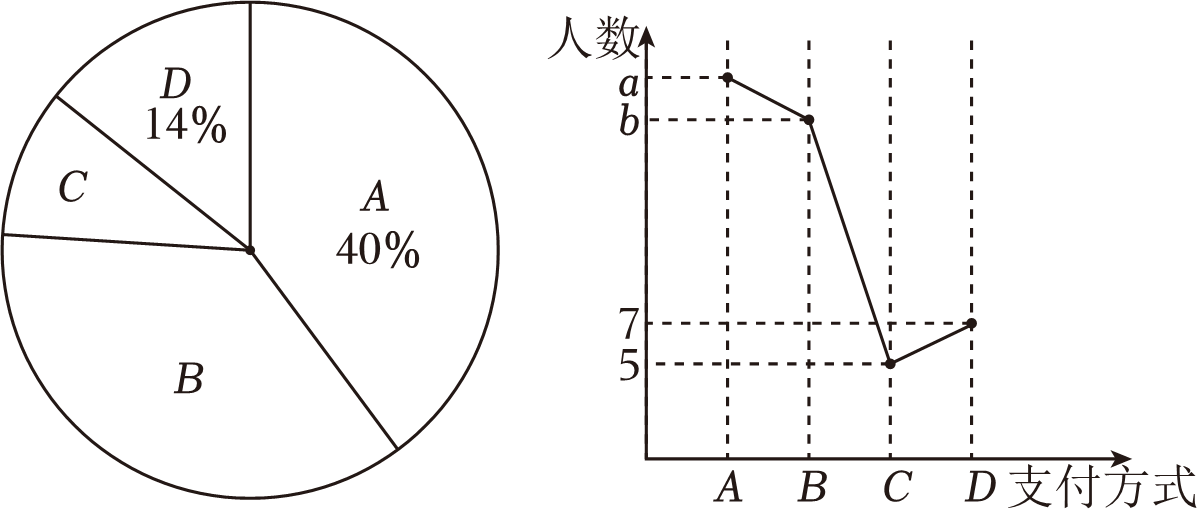
根据统计图表中的信息，解答下列问题：
1. （1） a＝，b＝，在扇形统计图中C种支付方式所对应的圆心角为度；
2. （2）本次调查中用现金支付方式的居民里有2名男性，其余都是女性，现从该种支付方式中随机选2名居民参加线上支付方式培训，求恰好都是女性的概率．
答案解析收藏纠错 + 选题
22. (2023九上·宁阳期中) 如图，在平面直角坐标系 $\text{[math]}$ 中，O为坐标原点，直线 $\text{[math]}$ 交y轴于点A ，交x轴于点B ，与双曲线 $\text{[math]}$ 在一，三象限分别交于C ， D两点， $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求k的值；
2. （2）求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
23. 如图，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的直径，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ 若 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 为 $\text{[math]}$ 的切线．
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的半径．
答案解析收藏纠错 + 选题
24. (2017·湖州) 湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了 $\text{[math]}$ $\text{[math]}$ 淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养 $\text{[math]}$ 天的总成本为 $\text{[math]}$ 万元；放养 $\text{[math]}$ 天的总成本为 $\text{[math]}$ 万元（总成本=放养总费用+收购成本）．
1. （1）设每天的放养费用是 $\text{[math]}$ 万元，收购成本为 $\text{[math]}$ 万元，求 $\text{[math]}$ 和 $\text{[math]}$ 的值；
2. （2）
  设这批淡水鱼放养 $\text{[math]}$ 天后的质量为 $\text{[math]}$ （ $\text{[math]}$ ），销售单价为 $\text{[math]}$ 元/ $\text{[math]}$ ．根据以往经验可知： $\text{[math]}$ 与 $\text{[math]}$ 的函数关系为 $\text{[math]}$ ； $\text{[math]}$ 与 $\text{[math]}$ 的函数关系如图所示．
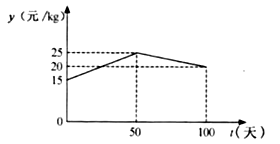
  ①分别求出当 $\text{[math]}$ 和 $\text{[math]}$ 时， $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式；
  ②设将这批淡水鱼放养 $\text{[math]}$ 天后一次性出售所得利润为 $\text{[math]}$ 元，求当 $\text{[math]}$ 为何值时， $\text{[math]}$ 最大？并求出最大值．（利润=销售总额-总成本）
答案解析收藏纠错 + 选题
25. (2023·济南) 在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，将射线 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转90°，交 $\text{[math]}$ 延长线于点 $\text{[math]}$ ，以线段 $\text{[math]}$ ， $\text{[math]}$ 为邻边作矩形 $\text{[math]}$ ．
1. （1）如图1，连接 $\text{[math]}$ ，求 $\text{[math]}$ 的度数和 $\text{[math]}$ 的值；
2. （2）如图2，当点 $\text{[math]}$ 在射线 $\text{[math]}$ 上时，求线段 $\text{[math]}$ 的长；
3. （3）如图3，当 $\text{[math]}$ 时，在平面内有一动点 $\text{[math]}$ ，满足 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的最小值．
答案解析收藏纠错 + 选题
26. (2023九上·义乌月考) 如图，抛物线 $\text{[math]}$ 的图象经过 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点，且一次函数 $\text{[math]}$ 的图象经过点B.
1. （1）求抛物线和一次函数的解析式.
2. （2）点E，F为平面内两点，若以E、F、B、C为顶点的四边形是正方形，且点E在点F的左侧.这样的E，F两点是否存在？如果存在，请直接写出所有满足条件的点E的坐标：如果不存在，请说明理由.
3. （3）将抛物线 $\text{[math]}$ 的图象向右平移8个单位长度得到抛物线 $\text{[math]}$ ，此抛物线的图象与x轴交于M，N两点（M点在N点左侧）.点P是抛物线 $\text{[math]}$ 上的一个动点且在直线 $\text{[math]}$ 下方.已知点P的横坐标为m.过点P作 $\text{[math]}$ 于点D.求m为何值时， $\text{[math]}$ 有最大值，最大值是多少？
答案解析收藏纠错 + 选题