2024年浙教版数学八（下）微素养核心突破18 正方形与全等...

更新时间：2024-06-03 浏览次数：22 类型：复习试卷

一、选择题

1. 如图，正方形ABCD的边长为 10，AG=CH=8，BG=DH=6，连结GH，则GH 的长为（）

A . $\text{[math]}$ B . 2 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 如图，正方形ABCD的对角线AC，BD相交于点O，M是边AD上一点，连结OM，过点O作ON⊥OM，交CD于点N．若四边形MOND的面积是1，则AB的长为（）

A . 1 B . $\text{[math]}$ C . 2 D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023八下·阳西期末) 如图，在边长为3的正方形ABCD中， $\text{[math]}$ ，则BF的长是（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
4. (2024八下·荔湾期中) 如图，正方形ABCD的对角线AC，BD交于点O，M是边AD上一点，连接OM，过点O作ON⊥OM，交CD于点N．若四边形MOND的面积是1，则AB的长为（）

A . 1 B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. 如图，四边形ABCD是正方形，BE⊥EF，DF⊥EF，BE=2.5dm，DF=4dm，那么EF的长为（）

A . 6.5dm B . 6dm C . 5.5dm D . 4dm

答案解析收藏纠错 + 选题
6. (2022八下·高平期末) 如图，在正方形 $\text{[math]}$ 中，点P在边 $\text{[math]}$ 上， $\text{[math]}$ 于点E， $\text{[math]}$ 于点F，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
7. (2022八下·温岭期中) 如图，四边形ABCD是正方形，G是BC上的任意一点，DE⊥AG于点E，BF $\text{[math]}$ DE且交AG于点F，若AB = 4EF，则 $\text{[math]}$ S_正方形ABCD的值为（）

A . 9：16 B . 17：32 C . 17：36 D . 18：35

答案解析收藏纠错 + 选题
8. (2024八下·广州开学考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 的各边为边作三个正方形，点 $\text{[math]}$ 落在 $\text{[math]}$ 上，若 $\text{[math]}$ ，空白部分面积为 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023八下·双鸭山期中) 如图，边长为 $\text{[math]}$ 的正方形 $\text{[math]}$ 的对角线 $\text{[math]}$ 相交于点O，点G在 $\text{[math]}$ 边上，将正方形 $\text{[math]}$ 沿直线 $\text{[math]}$ 折叠，点C落在对角线 $\text{[math]}$ 上的点E处，折痕 $\text{[math]}$ 交 $\text{[math]}$ 于点M，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023八下·三台期中) 如图，在正方形ABCD中，O为对角线AC、BD的交点，E、F分别为边BC、CD上一点，且 $\text{[math]}$ ，连接EF ．若∠AOE＝150°， $\text{[math]}$ ，则EF的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题

二、填空题

11. (2023八下·东阳期末) 如图，正方形ABCD的对角线AC，BD相交于点O，AE平分∠BAC分别交BC，BD于点E，点M，过点B作BF⊥AE于点P，交AC于点G，交CD于点F，则OM与OG存在数量关系；当OM＝1时，则BM＝．

答案解析收藏纠错 + 选题
12. (2021八下·招远期中) 如图，小明同学将边长为5cm的正方形塑料模板ABCD与一块足够大的直角三角板叠放在一起，其中直角三角板的直角顶点落在点A处，两条直角边分别与CD交于点F，与CB延长线交于点E，则四边形AECF的面积是．

答案解析收藏纠错 + 选题
13. (2023八下·安达期末) 如图，直线l正方形ABCD的顶点B，点A、点C到直线l的距离分别是3和4，则该正方形的面积是.

答案解析收藏纠错 + 选题
14. (2023八下·宜兴月考) 如图，边长为2的正方形 $\text{[math]}$ 的对角线相交于点O，点E是 $\text{[math]}$ 边上的动点，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 的延长线于点P，过点O作 $\text{[math]}$ 交 $\text{[math]}$ 于点F，交 $\text{[math]}$ 延长线于点Q，连接 $\text{[math]}$ ．若点 $\text{[math]}$ 恰好是 $\text{[math]}$ 中点时，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2021八下·钦州期末) 如图，四边形ABCD是正方形，点E是边BC的中点，∠AEF＝90°，且EF交正方形外角的平分线CF于点F，已知正方形边长为4，则EF的长为 .

答案解析收藏纠错 + 选题
16. 正方形ABCD的边长为2，如图1，点E，F均在正方形内部，且BE=EF=FD，∠E=∠F=90°，则BE的长为；如图2，点G，H，I，J，K，L均在正方形内部，且BG=GH=HI=IJ=JK=KL=LD，∠G=∠H=∠I=∠J=∠K=∠L=90°，则BG的长为.

答案解析收藏纠错 + 选题

三、解答题

17.
1. （1）如图①，在正方形ABCD中，E为边CD上一点，连结AE，过点A作AF⊥AE交CB的延长线于点F，猜想AE与AF的数量关系，并说明理由；
2. （2）如图②，在(1)的条件下，连结AC，过点A作AM⊥AC交CB的延长线于点M ，观察并猜想CE与MF的数量关系，并说明理由．
答案解析收藏纠错 + 选题
18.
如图①，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形ABCD的外角∠DCG的平分线CF于点F．
1. （1）如图②，取AB的中点H，连结HE，求证：AE=EF．
2. （2）如图③，若点E是BC的延长线上(除点C外)的任意一点，其他条件不变，结论“AE=EF"仍然成立吗？如果成立，写出证明过程；如果不成立，请说明理由．
答案解析收藏纠错 + 选题
19. 如图所示，直线a经过正方形ABCD的顶点A，分别过正方形ABCD的顶点B，D作BF⊥a于点F，DE⊥a于点E，若DE=8，BF=5，求EF的长．

答案解析收藏纠错 + 选题
20. 如图，四边形ABCD是正方形，C是BC上任意一点，DE⊥AG于点E，BF∥DE，且交AG于点F．求证：DE-BF=EF．

答案解析收藏纠错 + 选题
21. 如图①，在正方形ABCD中，点O是对角线AC的中点，点P是线段AO上(不与点A，O重合)的一个动点，过点P作PE⊥PB且PE交边CD于点E．
1. （1）求证：PE=PB．
2. （2）如图②，若正方形ABCD的边长为2，过点E作EF⊥AC于点F，在点P运动的过程中，PF的长度是否发生变化？若不变，试求出这个不变的值；若变化，请说明理由．
3. （3）用等式表示线段PC，PA，CE之间的数量关系．
答案解析收藏纠错 + 选题
22. 如图，在正方形ABCD中，点E在边AD上(不与点A，点D重合)，连结BE，作 AG⊥BE于点F，交边 CD于点G，连结 CF.
1. （1）求证：BE=AG.
2. （2）已知E 是边AD 的中点，AD=10.
  ①分别求AF，BF的长.
  ②求证：CB=CF.
答案解析收藏纠错 + 选题
23. (2023八下·宾阳期末)
1. （1）如图1，四边形 $\text{[math]}$ 是正方形，点G是边 $\text{[math]}$ 的中点， $\text{[math]}$ ，且 $\text{[math]}$ 交正方形外角 $\text{[math]}$ 的平分线 $\text{[math]}$ 于点F ，求证： $\text{[math]}$ .
  小明展示了一种正确的解题思路：取 $\text{[math]}$ 的中点M ，连接 $\text{[math]}$ ，请你写出证明过程．
2. （2）如图2，如果把“点G是 $\text{[math]}$ 边的中点”改为“点G是 $\text{[math]}$ 边上（除A、B外）的任意一点”，其他条件不变，那么结论“ $\text{[math]}$ ”仍然成立．这个结论正确吗？如果正确，写出证明过程；如果不正确，请说明理由；
3. （3）若点G在 $\text{[math]}$ 边的延长线上的任意一点，其他条件不变，结论“ $\text{[math]}$ .”仍然成立，你认为（1）的结论还正确吗？如果正确，写出证明过程；如果不正确，请说明理由.
答案解析收藏纠错 + 选题

四、综合题

24. (2023八下·西青期中) 如图，在正方形 $\text{[math]}$ 中，E是边 $\text{[math]}$ 上的一点，F是边 $\text{[math]}$ 延长线上的一点，且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
25. (2023八下·庐江期中) 如图1，在正方形 $\text{[math]}$ 中，点E在 $\text{[math]}$ 上，点F在 $\text{[math]}$ 的延长线上， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）连接 $\text{[math]}$ ，若 $\text{[math]}$ ，请利用图2验证勾股定理．
答案解析收藏纠错 + 选题
26. (2023八下·杭州期中) 四边形 $\text{[math]}$ 为正方形，E为对角线 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ．
1. （1）如图1，求证： $\text{[math]}$ ；
2. （2）如图2，过点E作 $\text{[math]}$ ，交边 $\text{[math]}$ 于点F，以 $\text{[math]}$ 为邻边作矩形 $\text{[math]}$ ．
  ①求证：矩形 $\text{[math]}$ 是正方形；
  ②若正方形 $\text{[math]}$ 的边长为6， $\text{[math]}$ ，求正方形 $\text{[math]}$ 的边长．
答案解析收藏纠错 + 选题
27. (2022八下·梁溪期中) 如图，点E，F分别在正方形ABCD的边CD，BC上，且DE=CF，点P在射线BC上（点P不与点F重合）.将线段EP绕点E顺时针旋转90得到线段EG，过点E作GD的垂线QH，垂足为点H，交射线BC于点Q.
1. （1）如图①，若点E是CD的中点，点P在线段BF上，则线段BP，QC，EC的数量关系为；
2. （2）如图②，若点E不是CD的中点，点P在线段BF上，判断（1）中的结论是否仍然成立.若成立，请写出证明过程；若不成立，请说明理由；
3. （3）若正方形ABCD的边长为6，AB=3DE，CQ=1，请直接写出线段BP的长.
答案解析收藏纠错 + 选题
28. (2018八下·扬州期中) 从反思中总结基本活动经验是一个重要的学习方法．例如，我们在全等学习中所总结的“一线三等角、K型全等”这一基本图形，可以使得我们在观察新问题的时候很自然地联想，借助已有经验，迅速解决问题．
1. （1）如图1，在平面直角坐标系中，四边形OBCD是正方形，且D（0，2），点E是线段OB延长线上一点，M是线段OB上一动点（不包括点O、B），作MN⊥DM，垂足为M，且MN=DM．
  设OM=a，请你利用基本活动经验直接写出点N的坐标（用含a的代数式表示）；
2. （2）如果（1）的条件去掉“且MN=DM”，加上“交∠CBE的平分线与点N”，如图2，求证：MD = MN．如何获得问题的解决，不妨在OD上取一点G，连接MG，设法构造△MDG与△NMB全等，请你按此思路证明：MD = MN．
3. （3）如图3，（2）的条件下请你继续探索：连接DN交BC于点F，连接FM，下列两个结论：①FM的长度不变；②MN平分∠FMB，请你指出正确的结论，并给出证明.
答案解析收藏纠错 + 选题

五、实践探究题

29. (2023八下·湖北期末) 综合与实践
1. （1）【教材情境】
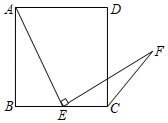
  数学活动课上，老师出示了一个问题：如图1，在正方形 $\text{[math]}$ 中，E是BC的中点， $\text{[math]}$ ， EP与正方形的外角 $\text{[math]}$ 的平分线交于P点．试猜想AE与EP的数量关系，并加以证明；同学们发现，取AB的中点F，连接EF可以解决这个问题，请在图1中补全图形，解答老师提出的问题．
2. （2）【实践探究】
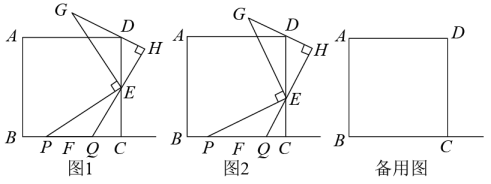
  “希望小组”受此问题启发，逆向思考这个题目，并提出新的问题：如图2，在正方形 $\text{[math]}$ 中，E为BC边上一动点（点E，B不重合），△AEP是等腰直角三角形， $\text{[math]}$ ，连接CP，可以求出 $\text{[math]}$ 的大小，请你思考并解答这个问题．
3. （3）【拓展迁移】
  “突击小组”深入研究“希望小组”提出的这个问题，发现并提出新的探究点：如图3，在正方形 $\text{[math]}$ 中，E为BC边上一动点（点E，B不重合），△AEP是等腰直角三角形， $\text{[math]}$ ，连接DP．知道正方形的边长时，可以求出△ADP周长的最小值．当 $\text{[math]}$ 时，△ADP周长的最小值为．（直接写出结果）
答案解析收藏纠错 + 选题