新人教版数学七上复习：一元一次方程的实际应用

更新时间：2024-07-02 浏览次数：8 类型：复习试卷

一、选择题

1. (2024七上·光明期末) 某项工程由甲单独做需12天完成，由乙单独做需8天完成，若甲、乙共同做，则它们完成这项工程的时间是（）天．

A . 20 B . $\text{[math]}$ C . 12 D . 8

答案解析收藏纠错 + 选题
2. (2024七上·高州期末) 墙上钉着用一根彩绳围成的梯形状的饰物，如图实线所示(单位：cm).小颖将梯形下底的钉子去掉，并将这条彩绳钉成一个长方形，如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm，根据题意，可得方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020七上·玉山期末) 张东同学想根据方程10x＋6＝12x－6编写一道应用题：“几个人共同种一批树苗，________，求参与种树的人数．”若设参与种树的有x人，那么横线部分的条件应描述为(　　)

A . 如果每人种10棵，那么缺6棵树苗；如果每人种12棵，那么剩下6棵树苗未种 B . 如果每人种10棵，那么剩下6棵树苗未种；如果每人种12棵，那么缺6棵树苗 C . 如果每人种10棵，那么剩下6棵树苗未种；如果每人种12棵，也会剩下6棵树苗未种 D . 如果每人种10棵，那么缺6棵树苗；如果每人种12棵，同样也是缺6棵树苗

答案解析收藏纠错 + 选题
4. 某商场购进一批服装，每件进价为1000元，由于换季滞销，商场决定将这种服装重新标价后按标价的7折销售．若想打折后每件服装仍能获利5%，该服装的标价应是（）

A . 1500元 B . 1400元 C . 1300元 D . 1200元

答案解析收藏纠错 + 选题
5. (2023七上·江油月考) 在某年全国足球甲级A组的前11场比赛中，某队保持连续不败，共积23分，按比赛规则，胜一场得3分，平一场得1分，那么该队共平了（）场比赛．

A . 7 B . 6 C . 5 D . 4

答案解析收藏纠错 + 选题
6. (2024七上·新昌期末) 甲乙丙三位同学合乘一辆滴滴车去顺路的三个地点，事先约定三人根据路程分摊车费，甲在全程的四分之一处下车，甲下车时，乙离下车点还有一半的路程，丙坐完全程．已知乙支付了18元车费，则三人一共支付多少车费？（）．

A . 36元 B . 48元 C . 63元 D . 81元

答案解析收藏纠错 + 选题
7. (2024七上·黔南期末) 如图，是 $\text{[math]}$ 年 $\text{[math]}$ 月的月历，任意选取“十”字型中的五个数 $\text{[math]}$ 比如图中阴影部分 $\text{[math]}$ ，若移动“十”字型后所得五个数之和为 $\text{[math]}$ ，那么该“十”字型中正中间的号数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024七上·杭州月考) 某小组计划做一批中国结，如果每人做6个，那么比计划多做了9个，如果每人做4个，那么比计划少7个．设计划做x个“中国结”，可列方程（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 程大位《直指算法统宗》：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁．意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完．试问大、小和尚各多少人？设大和尚有x人，依题意列方程得（）

A . $\text{[math]}$ +3（100﹣x）=100 B . $\text{[math]}$ ﹣3（100﹣x）=100 C . 3x+ $\text{[math]}$ =100 D . 3x﹣ $\text{[math]}$ =100

答案解析收藏纠错 + 选题
10. (2024七上·讷河期末) 中国有着5000年的灿烂文化，学习和了解中国古代数学文化是每一个中学生的责任，《九章算术》约成书于东汉，分九章介绍了许多算术及其解法，方程篇中有这样一道题：“今有乘传委输空车日行七十里，重车日行五十里．今载太仓粟输上林五日三返．”意思是说：驾马车在驿站间运送货物，空车一日行70里，重车一日行50里．现在从太仓运谷子到上林，5日往返3次．根据题意，下面所列方程正确的是（）

A . 设太仓到上林的距离为x里， $\text{[math]}$ B . 设太仓到上林的距离为x里， $\text{[math]}$ C . 设重车行驶x天， $\text{[math]}$ D . 设重车行驶x天， $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023七上·南岗月考) 某商店在某一时间以每件180元的价格卖出两件衣服，其中一件盈利20%，另一件亏损10%，该商店卖出这两件衣服共盈利元．

答案解析收藏纠错 + 选题
12. (2024七上·磐石期末) 一列火车匀速行驶，经过一条长 $\text{[math]}$ 米的隧道需要 $\text{[math]}$ 秒的时间，隧道的顶部一盏固定灯，在火车上垂直照射的时间为 $\text{[math]}$ 秒，则火车的长为米．

答案解析收藏纠错 + 选题

13. (2023七上·黄石港期末) 某市近期公布的居民用天然气阶梯价格方案如下：

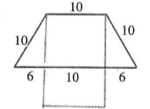
第一档天然气用量	第二档天然气用量	第三档天然气用量
年用天然气量360立方米及以下，价格为每立方米2元	年用天然气量超出360立方米，不足600立方米时，超过360立方米部分每立方米价格为2.5元．	年用天然气量600立方米以上，超过600立方米部分价格为每立方米3元．

若某户2023年实际缴纳天然气费2463元，则该户2023年使用天然气立方米．

答案解析收藏纠错 + 选题

14. (2024七上·拱墅期末) 有两所图书馆，自建馆以来每年各进图书0.5万册，若今年甲馆共有藏书27万册，乙馆共有藏书11万册，从今年起，n年后甲馆的藏书是乙馆的2倍，则n=.

答案解析收藏纠错 + 选题
15. (2024七上·诸暨期末) 第十九届亚运会于2023年9月23 日至 2023 年 10月8日在杭州举行．中国运动员发扬顽强拼搏，敢于争先的精神，在比赛场上屡创佳绩，获得金，银，铜牌共383枚，其中金牌比银牌的2 倍少 21枚，铜牌比银牌少40 枚，则中国运动员获得的金牌数是．

答案解析收藏纠错 + 选题

三、解答题

16. (2024七上·萧山期末) 一根竹竿插入一水池底部的淤泥中（如图），竹竿的入泥部分占全长的 $\text{[math]}$ ，淤泥以上的入水部分比入泥部分长 $\text{[math]}$ 米，露出水面部分为 $\text{[math]}$ 米，竹竿有多长？水有多深？

答案解析收藏纠错 + 选题

17. (2024七上·嵊州期末) 根据下面柔柔和小齐的对话，请计算小齐买平板电脑的预算．

柔柔：小齐，你之前提到的平板电脑买了没？

小齐：还没，它的售价比我的预算多1000元呢！

柔柔：这台平板电脑现在正在打7折呢！

小齐：是嘛，太好了，这样比我的预算还要少500元！

答案解析收藏纠错 + 选题

18. (2023七上·福田月考) $\text{[math]}$ ， $\text{[math]}$ 两地相距 $\text{[math]}$ 千米，甲骑自行车从 $\text{[math]}$ 地前往 $\text{[math]}$ 地，速度为每小时 $\text{[math]}$ 千米， $\text{[math]}$ 小时后，乙骑摩托车也沿相同的路线从 $\text{[math]}$ 地前往 $\text{[math]}$ 地，速度为每小时 $\text{[math]}$ 千米．
1. （1）乙出发多长时间后能追上甲？
2. （2）若乙到达 $\text{[math]}$ 地后立即返回，返回途中与甲相遇的地点距 $\text{[math]}$ 地多少千米？
答案解析收藏纠错 + 选题
19. (2024七上·金沙月考) 某电商销售A ， B两种产品，相关信息如下表．

进价（元/件）
售价（元/件）
A种产品
30
45
B种产品
40
60
1. （1）该电商十月份售出了A ， B两种产品共840件，总利润是15600元，该电商十月份售出A ， B两种产品各多少件？（利润=售价-进价）
2. （2）该电商在“双十一”期间采取了以下优惠方案：A种产品实行“买五免一”的成组销售优惠活动（每5件商品为一组，每买5件商品，其中1件商品免费），B种产品打八五折．
  ①A种产品实行的“买五免一”优惠活动，相当于每件A种产品打折销售．
  ②该电商“双十一”期间售出了A种产品500件，B种产品若干件，且总利润比十月份增加了5000元，则该电商“双十一”期间售出了B种产品多少件？
答案解析收藏纠错 + 选题

20. (2024七上·越城期末) 一家电信公司推出如下两种移动电话计费方式：

类别	计费方式
计费方式 $\text{[math]}$	每月收月租费58元，通话时间不超过150分钟的部分免费，超过150分钟部分按每分钟 $\text{[math]}$ 元加收通话费．
计费方式 $\text{[math]}$	每月收月租费88元，通话时间不超过350分钟的部分免费，超过350分钟部分按每分钟 $\text{[math]}$ 元加收通话费．

（1）若一个月通话时间为250分钟，则 $\text{[math]}$ ， $\text{[math]}$ 两种计费方式相差多少元？
（2）小敏爸爸选用计费方式 $\text{[math]}$ ，小聪爸爸选用计费方式 $\text{[math]}$ ，他们一个月里通话时间正好相同，但他俩的通话费用却相差25元．试求出他俩一个月的实际通话时间．

答案解析收藏纠错 + 选题

21. (2024七上·杭州月考) 用A，B两种型号的机器生产相同的产品，产品装入同样规格的包装箱后运往仓库．已知每台B型机器比A型机器一天多生产2件产品，3台A型机器一天生产的产品恰好能装满5箱，4台B型机器一天生产的产品恰好能装满7箱．每台A型机器一天生产多少件产品？每箱装多少件产品？

下面是解决该问题的两种方法，请选择其中的一种方法，完成分析填空和解答．

【方法一】分析：设每箱装x件产品，则3台A型机器一天共生产① ▲ )件产品，4台B型机器一天共生产( ▲ )件产品，再根据题意列方程．

解：设每箱装x件产品．

答：（写出完整的解答过程）

【方法二】分析：设每台A型机器一天生产x件产品，则每台B型机器一天生产（x+2）件产品，3台A型机器一天共生产(① ▲ )件产品，4台B型机器一天共生产(② ▲ )件产品，再根据题意列方程．

解：设每台A型机器一天生产x件产品

答：（写出完整的解答过程）

答案解析收藏纠错 + 选题

22. (2024七上·播州期末) 在数轴上，点A在原点右边，距原点5个单位长度，点B在点A的左边，与点A相距25个单位长度，点M从点A出发，以每秒4个单位的速度在 $\text{[math]}$ 之间往返运动，点N从点B出发，以一定的速度向右运动．
1. （1）点A表示的数为，点B表示的数为．
2. （2）当点N从点B处出发2秒后，点M才开始运动，点M运动4秒后， $\text{[math]}$ 第一次相遇，求点N的运动速度．
3. （3）在（2）的情况下，点 $\text{[math]}$ 继续运动t秒，当其中一个点运动到点A时，点 $\text{[math]}$ 均停止运动，当点 $\text{[math]}$ 之间的距离为4个单位长度时，求t的值．
答案解析收藏纠错 + 选题
23. (2024七上·黔西南期末) 如图1，大课间的广播操展让我们充分体会到了一种整体的图形之美，洋洋和乐乐想从数学角度分析下如何能让班级同学们的广播操做得更好，他们搜集了标准广播操图片进行讨论，如图2，为了方便研究，定义两手手心位置分别为A ， B两点，两脚脚跟位置分别为C ， D两点，定义A ， B ， C ， D平面内O为定点，将手脚运动看作绕点O进行旋转：
1. （1）填空：如图2，A ， O ， B三点共线，且∠AOC＝∠BOC ，则∠AOC＝°；
2. （2）第三节腿部运动中，如图3，洋洋发现，虽然A ， O ， B三点共线，却不在水平方向上，且∠AOD：∠BOC＝3：2．他经过计算发现，∠AOC﹣ $\text{[math]}$ ∠BOD的值为定值，请判断洋洋的发现是否正确，如果正确请求出这个定值，如果不正确，请说明理由；
3. （3）第四节体侧运动中，乐乐发现，两腿左右等距张开且∠COD＝30°，开始运动前A、O、B三点在同一水平线上，OA、OB绕点O顺时针旋转，OA旋转速度为50°/s ， OB旋转速度为25°/s ，当OB旋转到与OD重合时，运动停止，如图4．
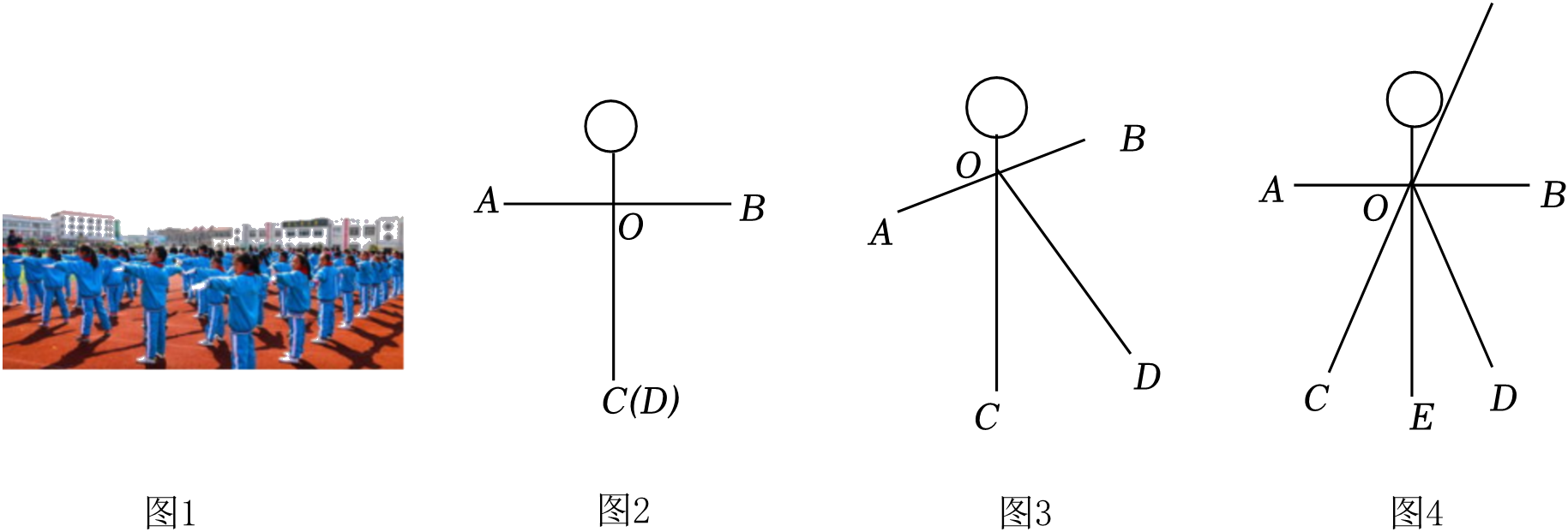
  ①运动停止时，直接写出∠AOD＝　▲　；
  ②请帮助乐乐求解运动过程中∠AOC与∠BOE的数量关系．
答案解析收藏纠错 + 选题

四、实践探究题

24. (2024七上·温州期末) 综合与实践：设计完成工程的最短工期方案（最短工期是指完成某项工程所需的最短时间）．
【背景素材】某公司要生产某大型产品60件，已知甲，乙，丙三家子工厂完成一件产品的时间分别为4天，6天，5天．现计划：①三家子工厂同时开始生产；②分配给甲工厂的数量是丙的2倍．
【问题解决】为设计方案，可以通过特殊情况或满足部分条件逐步进行探究．
1. （1）思考1（特值分析）：若该公司将20件产品分配给甲工厂，则最短工期为多少天？
2. （2）思考2（减少要素）：若不考虑素材②，仅由甲、乙两工厂完成，则当两家工厂同时完成生产时工期最短，求如何分配产品件数与最短工期．
3. （3）思考3（方案探究）：如何分配三家工厂的生产任务使得工期最短，并求出最短工期．（注：如你直接挑战思考3并正确解答也给满分）
答案解析收藏纠错 + 选题

25. (2024七上·婺城期末) 根据以下素材，探索完成任务．

时钟里的数学问题
素材1	时钟是我们口常生活中常用的生活用品。钟表上的时针和分针都绕其轴心旋转，如图．表盘中1-12匀分布，分针60分钟转动一周是360°，时针60分钟移动一周的 $\text{[math]}$ 是30°，这样，分针转速为每分钟转6度，时针转速为每分钟转0.5度．
素材2	当时钟显示10：10时（如图）．时针与分针所成角度多少度？解决这个问题，可以先考虑10：00时，时针与分针所成角度为60°；从10：00到10：10．分针转动的角度为 $\text{[math]}$ ．时针转动的角度为 $\text{[math]}$ ， $\text{[math]}$ ．因此10点10分时，时针与分针所成角度是115°．
素材3	当时针和分针所成角度180°时，我们将这样的时刻称为“美妙时刻”。如图．当时钟显示6：00时，此时，时针和分针所成角度180°，因此6：00就是一个美妙时刻．
解决问题
任务1	当时钟显示1：10分时，求时针与分针所成角度．
任务2	时钟显示1：00时，时针与分针所成角度为30°，在1：00到1：30的30分钟内，小明发现存在着时针和分针册直的情况，请求出此时的时刻。
任务3	6：00之后的下一个美妙时刻是 ▲ ，一天24个小时内，共有 ▲ 个美妙时刻。

答案解析收藏纠错 + 选题

26. (2024七上·吴兴期末) 根据以下素材，回答问题．

问题背景	吴兴区某学校决定在校内开辟劳动实践基地，现向全校师生征集实践基地的设计方案．学校项目化学习小组根据学校要求完成了初步设计，请跟随小组成员共同完成以下任务．
素材一	项目化学习小组通过初步研讨，计划利用学校现成的一堵“L”型墙面和栅栏围成长方形的劳动实践基地BFED，其中粗线A-B-C表示墙面，已知AB⊥BC，AB＝2米，BC＝6米.初步设计方案有两种：如图①，点D在线段BC上；如图②，点D在线段BC的延长线上（包括点C）．
素材二	通过查询学校现有物资信息，学校仓库可提供栅栏的总长度为10米.项目化学习小组决定将这10米栅栏全部用于劳动实践基地中.
素材三	经过市场调查，建造劳动实践基地的人工和材料费合计为25元/平方米.