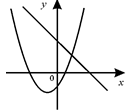
 B .
B . 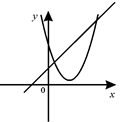 C .
C . 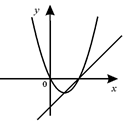 D .
D . 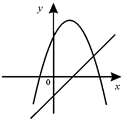


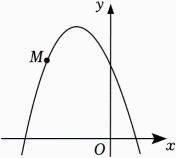

如何设计喷泉安全通道? 在抛物线形的喷泉水柱下设置一条安全的通道,可以让儿童在任意时间穿过安全通道时不被水柱喷到(穿梭过程中人的高度变化忽略不计). | ||
素材1 | 图1为音乐喷泉,喷头的高度在垂直地面的方向上随着音乐变化而上下移动.不同高度的喷头喷出来的水呈抛物线型或抛物线的一部分,但形状相同,最高高度也相同,水落地点都在喷水管的右侧. |
|
素材2 | 图2是当喷水头在地面上时(喷水头最低),其抛物线形水柱的示意图,水落地点离喷水口的距离为 图3是某一时刻时,水柱形状的示意图. |
|
素材3 | 安全通道 |
|
问题解决 | ||
任务1 | 确定喷泉形状. | 在图2中,以 标系,求出抛物线的函数表达式. |
任务2 | 确定喷泉跨度的最小值. | 若喷水管 |
任务3 | 设计通道位置及儿童的身高上限. | 现在需要一条宽为
的最大身高为多少?(精确到 |