人教版九年级上学期数学第二十三章质量检测（高阶）

更新时间：2024-09-12 浏览次数：20 类型：单元试卷

一、选择题（每题3分，共30分）

1. (2024九上·萧山月考) 如图，将含有 $\text{[math]}$ 角的直角三角板 $\text{[math]}$ 放置在平面直角坐标系中， $\text{[math]}$ 在x轴上，若 $\text{[math]}$ ，将三角板绕原点O顺时针旋转 $\text{[math]}$ ，则点A的对应点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九上·武昌月考) 如图，平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是边 $\text{[math]}$ 上一点，且 $\text{[math]}$ ， $\text{[math]}$ 是边 $\text{[math]}$ 上的一个动点，将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 14 D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九上·游仙期末) 如图，边长为12的等边三角形ABC中，M是高CH所在直线上的一个动点，连结MB ，将线段BM绕点B逆时针旋转60°得到BN ，连结HN ．则在点M运动过程中，线段HN长度的最小值是（）

A . 6 B . 3 C . 2 D . 1.5

答案解析收藏纠错 + 选题
4. (2024九上·丰台期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， D为 $\text{[math]}$ 边上一点，将 $\text{[math]}$ 绕点A逆时针旋转90°得到 $\text{[math]}$ ，点B、D的对应点分别为点C、E，连接 $\text{[math]}$ ，将 $\text{[math]}$ 平移得到 $\text{[math]}$ （点A、C的对应点分别为点D、F），连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . 6 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八上·翠屏月考) 如图，O是等边 $\text{[math]}$ 内一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，将线段BO以点B为旋转中心逆时针旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ ，下列结论：① $\text{[math]}$ 可以由 $\text{[math]}$ 绕点B逆时针旋转 $\text{[math]}$ 得到；②点O与 $\text{[math]}$ 的距离为4；③点 $\text{[math]}$ ；④ $\text{[math]}$ ；⑤ $\text{[math]}$ ．其中正确的有多少（　　）个

A . 5 B . 4 C . 3 D . 2

答案解析收藏纠错 + 选题
6. (2023九上·开江月考) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ 、 $\text{[math]}$ 是射线 $\text{[math]}$ 上的动点，且 $\text{[math]}$ ，射线 $\text{[math]}$ 、 $\text{[math]}$ 分别交 $\text{[math]}$ 、 $\text{[math]}$ 延长线于 $\text{[math]}$ 、 $\text{[math]}$ ，连接 $\text{[math]}$ ，在下列结论中：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④若 $\text{[math]}$ ，则 $\text{[math]}$ ，
⑤ $\text{[math]}$ ，其中正确的结论有（）

A . $\text{[math]}$ 个 B . $\text{[math]}$ 个 C . $\text{[math]}$ 个 D . $\text{[math]}$ 个

答案解析收藏纠错 + 选题
7. (2023九上·北关期中) 如图，菱形 $\text{[math]}$ 的顶点O与原点重合，点C在x轴上，点A的坐标为 $\text{[math]}$ ，将菱形 $\text{[math]}$ 绕点O逆时针旋转，每次旋转 $\text{[math]}$ ，则第 $\text{[math]}$ 次旋转结束时，点B的坐标为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·滨州期中) 如图，正方形ABCD的边长为4，对角线AC、BD相交于点O，将△ABD绕着点B顺时针旋转45°得到△BEF，EF交CD于点G，连接BG交AC于点H，连接EH．则下列结论：①△BGE≌△BGC；②四边形EHCG是菱形；③△BDG的面积是8﹣4 $\text{[math]}$ ；④OH＝4﹣2 $\text{[math]}$ ．其中正确结论的序号是（）
\

A . ①② B . ①②③ C . ①②④ D . ①②③④

答案解析收藏纠错 + 选题
9. (2023九上·温岭期中) 如图，在平面直角坐标系中，Rt△AOB的一条直角边OB在x轴上，点A的坐标为（-6，4）；Rt△COD中，∠COD＝90°，OD＝4 $\text{[math]}$ ， ∠D＝30°，连接BC，点M是BC中点，连接AM．将Rt△COD以点O为旋转中心按顺时针方向旋转，在旋转过程中，线段AM的最小值是（）

A . 3 B . 6 $\text{[math]}$ -4 C . 2 $\text{[math]}$ -2 D . 2

答案解析收藏纠错 + 选题
10. (2024九上·婺城开学考) 如图，已知在平面直角坐标系 $\text{[math]}$ 中，一段抛物线 $\text{[math]}$ ，记为抛物线 $\text{[math]}$ ，它与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ， $\text{[math]}$ ；将抛物线 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转 $\text{[math]}$ 得抛物线 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ， $\text{[math]}$ ；将抛物线 $\text{[math]}$ 绕点 $\text{[math]}$ ，旋转 $\text{[math]}$ 得抛物线 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ， $\text{[math]}$ ；……如此进行下去，得到一条“波浪线”，若点 $\text{[math]}$ 在此“波浪线”上，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 9 D . 5

答案解析收藏纠错 + 选题

二、填空题（每题3分，共15分）

11. (2024八下·渠县期中) 如图，已知△ABC ， ∠ABC＜60°，将△ABC绕点A逆时针旋转60°得到△ADE ， DE与BC交于点P ．下列结论：
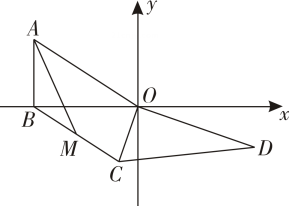
①∠EPC＝60°；
②AC与DE互相平分；
③PA+PC＝PE；
④PA平分∠BPE ，其中正确结论的是．

答案解析收藏纠错 + 选题
12. (2024九上·渠县期末) 如图，正方形 $\text{[math]}$ 中， $\text{[math]}$ ， O是 $\text{[math]}$ 边的中点，点E是正方形内一动点， $\text{[math]}$ ，连接 $\text{[math]}$ ，将线段 $\text{[math]}$ 绕点D逆时针旋转 $\text{[math]}$ 得 $\text{[math]}$ ，连接 $\text{[math]}$ ，则线段 $\text{[math]}$ 长的最小值为．

答案解析收藏纠错 + 选题
13. (2023九上·番禺期中) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ， F是边 $\text{[math]}$ 上的动点，将 $\text{[math]}$ 绕点A顺时针旋转 $\text{[math]}$ 至 $\text{[math]}$ ，将 $\text{[math]}$ 沿AF翻折至 $\text{[math]}$ ，连接 $\text{[math]}$ 交于点H，连接 $\text{[math]}$ ，则 $\text{[math]}$ 面积的最大值为．

答案解析收藏纠错 + 选题
14. (2023九上·唐河期中) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， F为 $\text{[math]}$ 中点，P是线段 $\text{[math]}$ 上一点，设 $\text{[math]}$ ，连结 $\text{[math]}$ 并将它绕点P顺时针旋转90°得到线段 $\text{[math]}$ ，连结 $\text{[math]}$ 、 $\text{[math]}$ ，则在点P从点B向点C的运动过程中，有下面四个结论：①当 $\text{[math]}$ 时， $\text{[math]}$ ；②点E到边 $\text{[math]}$ 的距离为m；③直线 $\text{[math]}$ 一定经过点 $\text{[math]}$ ；④ $\text{[math]}$ 的最小值为 $\text{[math]}$ ．其中结论正确的是．（填序号即可）

答案解析收藏纠错 + 选题
15. (2021九上·柯桥月考) 如图，“心”形是由抛物线 $\text{[math]}$ 和它绕着原点O ，顺时针旋转60°的图形经过取舍而成的，其中顶点C的对应点为D ，点A ， B是两条抛物线的两个交点，点E ， F ， G是抛物线与坐标轴的交点，则AB= ．

答案解析收藏纠错 + 选题

三、作图题（共2题，共18分）

16. (2023九上·济宁月考) 如图，△ABC中， $\text{[math]}$ ， $\text{[math]}$ ，边BA绕点B顺时针旋转 $\text{[math]}$ 角得到线段BP，连接PA，PC，过点P作 $\text{[math]}$ 于点D．
1. （1）如图1，若 $\text{[math]}$ ， $\text{[math]}$ ______°；
2. （2）如图2，若 $\text{[math]}$ ，求∠DPC的度数；
3. （3）如图3，若 $\text{[math]}$ ，依题意补全图，并求出∠DPC的度数．
答案解析收藏纠错 + 选题
17. (2024九上·清城开学考) 如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
1. （1）请画出将△ABC向左平移4个单位长度后得到的图形△A₁B₁C₁；
2. （2）请画出△ABC关于原点O成中心对称的图形△A₂B₂C₂；
3. （3）在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标．
答案解析收藏纠错 + 选题

四、解答题（共5题，共45分）

18. (2024九上·馆陶期末) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，垂足为E ． F是点E关于 $\text{[math]}$ 的对称点，连接 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ $\text{[math]}$ ；
2. （2）求 $\text{[math]}$ 和 $\text{[math]}$ 的长；
3. （3）将一个与 $\text{[math]}$ 完全重合的透明三角板 $\text{[math]}$ 沿射线 $\text{[math]}$ 方向平移．
  ①设点 $\text{[math]}$ 在 $\text{[math]}$ 上移动的距离是m ．当点 $\text{[math]}$ 分别落在线段 $\text{[math]}$ 上时，求相应的m的值；
  ②当点 $\text{[math]}$ 落在 $\text{[math]}$ 上时，立刻将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转，且旋转60°时停止．点H在 $\text{[math]}$ 上，且 $\text{[math]}$ ．若 $\text{[math]}$ 平移的速度为每秒1个单位长度， $\text{[math]}$ 绕点 $\text{[math]}$ 旋转的速度为每秒5°，在 $\text{[math]}$ 整个运动过程中，直接写出点H在 $\text{[math]}$ 区域（含边界）内的时长．
答案解析收藏纠错 + 选题
19. (2023九上·赤坎期末) 如图，已知抛物线 $\text{[math]}$ （ $\text{[math]}$ ）与 $\text{[math]}$ 轴交于点 $\text{[math]}$ 和点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求此抛物线的解析式；
2. （2）若点 $\text{[math]}$ 为第二象限抛物线上一动点，连接 $\text{[math]}$ ， $\text{[math]}$ ，求四边形 $\text{[math]}$ 面积的最大值，并求出此时点 $\text{[math]}$ 的坐标；
3. （3）点 $\text{[math]}$ 在抛物线的对称轴上，若线段 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转90°后，点 $\text{[math]}$ 的对应点 $\text{[math]}$ 恰好也落在此抛物线上，求点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
20. (2024九上·兴国期末) 课本知识再现：
（Ⅰ）归纳（八年级上册课本 $\text{[math]}$ 页）：点 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的点的坐标为 $\text{[math]}$ ；点 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的点的坐标为 $\text{[math]}$ ；
（Ⅱ）归纳（九年级上册课本 $\text{[math]}$ 页）：两个点关于原点对称时，它们的坐标符号相反，即点 $\text{[math]}$ 关于原点的对称点为 $\text{[math]}$ ．
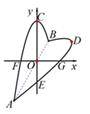
小颖在学习完《旋转》与《二次函数》两章后，从点的对称角度思考函数图象的对称，发现一次函数、二次函数图象上也可以应用点的对称特点．
根据上面知识，求与已知直线 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的直线的解析式；
解：设与直线 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的直线上任意一点 $\text{[math]}$ ，
∵点 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的点的坐标为 $\text{[math]}$ ，
又∵点 $\text{[math]}$ 必在直线 $\text{[math]}$ 上，
把点 $\text{[math]}$ 代入 $\text{[math]}$ ，得
$\text{[math]}$ ，
∴与已知直线 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的直线的解析式为 $\text{[math]}$ ．
理解上面的解题过程，并完成下题：
1. （1）直接写出直线 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的直线的解析式为　；
2. （2）已知二次函数 $\text{[math]}$ 的图像与抛物线 $\text{[math]}$ 关于原点对称，请根据上述方法求 $\text{[math]}$ 的值；
3. （3）判断以下每对函数的图象：
  ① $\text{[math]}$ 与 $\text{[math]}$ ；       ② $\text{[math]}$ 与 $\text{[math]}$ ；
  ③ $\text{[math]}$ 与 $\text{[math]}$ ；                    ④ $\text{[math]}$ 与 $\text{[math]}$ ．
  其中一定关于原点对称的是　       　（填序号）．
答案解析收藏纠错 + 选题
21. (2024九上·绵阳期末) 如图， $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点A逆时针旋转得到 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点D ， $\text{[math]}$ 与 $\text{[math]}$ 交于点E ， $\text{[math]}$ 与 $\text{[math]}$ 交于点F ，当B、D、F重合时停止旋转．
1. （1）证明：在旋转过程中 $\text{[math]}$ ；
2. （2）如图1，当 $\text{[math]}$ 平分 $\text{[math]}$ 时，证明： $\text{[math]}$ ；
3. （3）如图2，若 $\text{[math]}$ ， $\text{[math]}$ ，在旋转过程中，当 $\text{[math]}$ 是等腰三角形时，求该等腰三角形底边的长度．
答案解析收藏纠错 + 选题
22. (2024九上·绥中期末) 【问题初探】（1）如图1， $\text{[math]}$ 为等边三角形内一点，满足 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，试求 $\text{[math]}$ 的大小.李明同学的思路是：将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转60°，点 $\text{[math]}$ 的对应点为 $\text{[math]}$ ，画出旋转后的图形，再连接 $\text{[math]}$ .将求 $\text{[math]}$ 分成求 $\text{[math]}$ 和 $\text{[math]}$ 的和即可.请你按照李明同学给出的旋转的思路，求 $\text{[math]}$ 的大小；
【问题解决】（2）如图2，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 分别为 $\text{[math]}$ ， $\text{[math]}$ 边上的点，满足 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积；
【问题拓展】（3）如图3，在四边形 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.

答案解析收藏纠错 + 选题

五、实践探究题（共12分）

23. (2023九上·吉州月考) 问题解决
一节数学课上，老师提出了这样一个问题：如图①，点P是等边 $\text{[math]}$ 内的一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .你能求出 $\text{[math]}$ 的度数和等边 $\text{[math]}$ 的面积吗?小明通过观察、分析、思考，形成了如下思路：
如图①将 $\text{[math]}$ 绕点B逆时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，可得 $\text{[math]}$ 是等边三角形，根据勾股定理逆定理可得 $\text{[math]}$ 是直角三角形，从而使问题得到解决.
1. （1）结合小明的思路完成填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
2. （2）类比探究
  ①.如图②，若点P是正方形 $\text{[math]}$ 内一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数和正方形的面积.
  ②.如图③，若点P是正方形 $\text{[math]}$ 外一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数和正方形的面积.
答案解析收藏纠错 + 选题