【培优版】北师大版数学九年级上册4.2平行线分线段成比例 ...

更新时间：2024-09-28 浏览次数：2 类型：同步测试

一、选择题

1. (2021九上·拱墅期中) 如图，H是△ABC的重心，延长AH交BC于D，延长BH交AC于M，E是DC上一点，且DE∶EC＝5∶2，连结AE交BM于G，则BH∶HG∶GM等于（）

A . 7∶5∶2 B . 13∶5∶2 C . 5∶3∶1 D . 26∶10∶3

答案解析收藏纠错 + 选题
2. (2021九上·平阳月考) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，与对角线 $\text{[math]}$ 相交于点N，F是线段 $\text{[math]}$ 的中点，则 $\text{[math]}$ 为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2019九上·顺德期末) 如图，一人站在两等高的路灯之间走动， $\text{[math]}$ 为人 $\text{[math]}$ 在路灯 $\text{[math]}$ 照射下的影子， $\text{[math]}$ 为人 $\text{[math]}$ 在路灯 $\text{[math]}$ 照射下的影子．当人从点 $\text{[math]}$ 走向点 $\text{[math]}$ 时两段影子之和 $\text{[math]}$ 的变化趋势是（）

A . 先变长后变短 B . 先变短后变长 C . 不变 D . 先变短后变长再变短

答案解析收藏纠错 + 选题
4. AD是△ABC的中线，E是AD上一点，AE：ED=1：3，BE的延长线交AC于F，AF：FC=（）

A . 1：3 B . 1：4 C . 1：5 D . 1：6

答案解析收藏纠错 + 选题
5. (2023九上·浙江期中) 如图，△ABC中，∠A=90°，AB=6，BC=10，∠ABC的平分线交AC于点D，与BC的垂线CE相交于点E，过点D作DF⊥BC于点F，则BD：DE为（）

A . 3：2 B . 5：3 C . 4：3 D . 2：1

答案解析收藏纠错 + 选题

二、填空题

6. (2023九上·浙江期中) 如图，矩形纸片ABCD，点E在边AD上，连接BE，点F在线段BE上，且EF= $\text{[math]}$ BF，折叠矩形纸片使点C恰好落在点F处，折痕为DG，若AB=4，则折痕DG的长为.

答案解析收藏纠错 + 选题
7. (2022九上·温州开学考) 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示．将小正方形对角线EF双向延长，分别交边AB，和边BC的延长线于点G，H．若大正方形与小正方形的面积之比为5，GH＝2 $\text{[math]}$ ，则大正方形的边长为．

答案解析收藏纠错 + 选题
8. (2020九上·大邑期中) 如图，正方形ABCD的边长AB＝4，点E、F分别是CB，DC延长线上的点，连AF交CB于点G，若BE＝1，连接AE，且∠EAF＝45°，则AG长为.

答案解析收藏纠错 + 选题
9. (2023九上·哈尔滨月考) 如图，正方形 $\text{[math]}$ 中，E、F分别为 $\text{[math]}$ 、 $\text{[math]}$ 边的中点，连接 $\text{[math]}$ ，将正方形折叠，使点C落在 $\text{[math]}$ 上点P的位置，折痕 $\text{[math]}$ 交 $\text{[math]}$ 于点G ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

答案解析收藏纠错 + 选题

三、解答题

10. (2024九上·绿园期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 方向以每秒2个单位长度的速度向终点 $\text{[math]}$ 运动，点 $\text{[math]}$ 为线段 $\text{[math]}$ 的中点，过点 $\text{[math]}$ 向上作 $\text{[math]}$ ，且 $\text{[math]}$ ，以 $\text{[math]}$ 、 $\text{[math]}$ 为边作矩形 $\text{[math]}$ ．设点 $\text{[math]}$ 的运动时间为（t>0）秒．
1. （1）线段 $\text{[math]}$ 的长为（用含的代数式表示）．
2. （2）当点N恰好落在边 $\text{[math]}$ 上时，求的值．
3. （3）当点 $\text{[math]}$ 在 $\text{[math]}$ 内部时，设矩形 $\text{[math]}$ 与 $\text{[math]}$ 重叠部分图形的面积为 $\text{[math]}$ ，求 $\text{[math]}$ 与之间的函数关系式．
4. （4）当点 $\text{[math]}$ 恰好落在 $\text{[math]}$ 的角平分线上时，直接写出的值．
答案解析收藏纠错 + 选题
11. (2017九上·东莞月考) 已知：如图，AB⊥BD，CD⊥BD，垂足分别为B、D，AD和BC相交于点E，EF⊥BD，垂足为F，我们可以证明 $\text{[math]}$ 成立（不要求考生证明）．
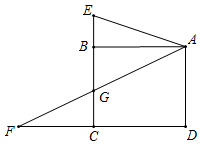
若将图中的垂线改为斜交，如图，AB∥CD，AD，BC相交于点E，过点E作EF∥AB交BD于点F，则：
1. （1） $\text{[math]}$ 还成立吗？如果成立，请给出证明；如果不成立，请说明理由；
2. （2）请找出S_△_ABD ， S_△_BED和S_△_BDC间的关系式，并给出证明．
答案解析收藏纠错 + 选题
12. (2023九上·资中期中) 阅读与计算，请阅读以下材料，完成相应的任务．
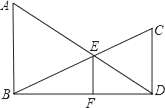
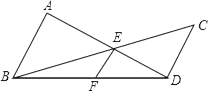
材料：三角形的内角平分线定理：
如图1，在 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，则 $\text{[math]}$ ．
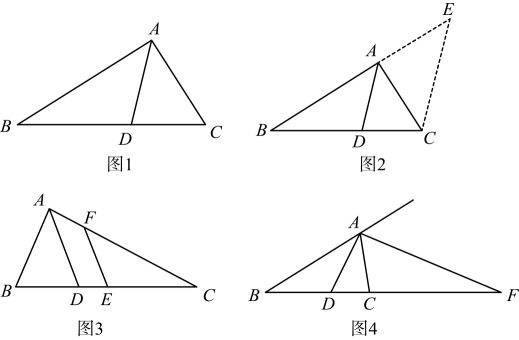
下面是这个定理的部分证明过程．
证明：如图2，过 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ．
1. （1）【思路说明】请按照上面的证明思路，写出该证明的剩余部分；
2. （2）【直接应用】如图3， $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 中点， $\text{[math]}$ 是 $\text{[math]}$ 的平分线， $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，求线段 $\text{[math]}$ 的长；
3. （3）【拓展延伸】如图4， $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 的延长线交 $\text{[math]}$ 外角角平分线 $\text{[math]}$ 于点 $\text{[math]}$ ．
  ①找出 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 这四条线段的比例关系，并证明；
  ②若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
13. (2020九上·乐平期末) 如图1，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，沿对角线 $\text{[math]}$ 剪开，再把 $\text{[math]}$ 沿 $\text{[math]}$ 方向平移得到图2，其中 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ．
1. （1）在图2中，除 $\text{[math]}$ 与 $\text{[math]}$ 外，指出图中全等三角形（不能添加辅助线和字母）并选择一对加以证明；
2. （2）设 $\text{[math]}$ ．
  ①当 $\text{[math]}$ 为何值时，四边形 $\text{[math]}$ 是菱形？
  
  ②设四边形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，求 $\text{[math]}$ 与 $\text{[math]}$ 的关系式，并求出 $\text{[math]}$ 最大值．
答案解析收藏纠错 + 选题
14. (2020九上·厦门月考) 如图， $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 的角平分线相交于点P，过点P作线 $\text{[math]}$ 分别交 $\text{[math]}$ 、 $\text{[math]}$ 于F，E．
1. （1）如图1，求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ 绕点P旋转，F在 $\text{[math]}$ 的延长线上滑动，如图2，请你测量，猜想 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的关系，写出这个关系式，并加以证明．
答案解析收藏纠错 + 选题