【培优版】北师大版数学九年级上册4.6利用相似三角形测高同...

更新时间：2024-09-30 浏览次数：9 类型：同步测试

一、选择题

1. 一块直角三角形木板，它的一条直角边AC长为1cm，面积为1cm² ，工人分别按图中甲、乙两种方式把它加工成一个正方形桌面，则正方形的面积较大的是（）.

A . 甲 B . 乙 C . 一样大 D . 无法判断

答案解析收藏纠错 + 选题
2. 如图，一张等腰三角形纸片，底边长为15cm，底边上的高线长为22.5cm．现沿底边依次从下往上裁剪宽度均为3 cm的矩形纸条，已知剪得的纸条中有一张是正方形，则这张正方形纸条是（）．

A . 第4张 B . 第5张 C . 第6张 D . 第7张

答案解析收藏纠错 + 选题
3. (2023九上·宁远期中) 如图，小明设计的用激光笔测量城墙高度的示意图，在点 $\text{[math]}$ 处水平放置一面平面镜，光线从点A出发经平面镜反射后刚好射到城墙 $\text{[math]}$ 的顶端 $\text{[math]}$ 处，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米，那么该城墙 $\text{[math]}$ 的高度为（）

A . 6 B . 8 C . 10 D . 18

答案解析收藏纠错 + 选题
4. (2024九上·长春汽车经济技术开发期末) 如图，某零件的外径为 $\text{[math]}$ ，用一个交叉卡钳 $\text{[math]}$ 可测量零件的内孔直径 $\text{[math]}$ 若 $\text{[math]}$ ： $\text{[math]}$ ： $\text{[math]}$ ，且量得 $\text{[math]}$ ，则零件的厚度 $\text{[math]}$ 为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·寿阳月考) 如图，某一时刻太阳光下，小明测得一棵树落在地面上的影子长为2.8米，落在墙上的影子高为1.2米，同一时刻同一地点，身高1.6米他在阳光下的影子长0.4米，则这棵树的高为（　　）米．

A . 6.2 B . 10 C . 11.2 D . 12.4

答案解析收藏纠错 + 选题
6. (2023九上·泗县月考) 如图，一间学在湖边看到一棵树，他目测出自己与树的距离为 $\text{[math]}$ ，低头观察湖面，看到树的顶端在水中的倒影距自己 $\text{[math]}$ 远．若该同学的眼睛到地面的距离为 $\text{[math]}$ ，则树高为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·运城期中) 据 $\text{[math]}$ 墨经 $\text{[math]}$ 记载，在两千多年前，我国学者墨子和他的学生做了“小孔成像”实验，阐释了光的直线传播原理 $\text{[math]}$ 小孔成像的示意图如图所示，光线经过小孔 $\text{[math]}$ ，物体 $\text{[math]}$ 在幕布上形成倒立的实像 $\text{[math]}$ 点 $\text{[math]}$ 、 $\text{[math]}$ 的对应点分别是 $\text{[math]}$ 、 $\text{[math]}$ 若物体 $\text{[math]}$ 的高为 $\text{[math]}$ ，小孔 $\text{[math]}$ 到地面距离 $\text{[math]}$ 为 $\text{[math]}$ ，则实像 $\text{[math]}$ 的高度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·新田月考) 如图， $\text{[math]}$ 为驾驶员的盲区，驾驶员的眼睛点 $\text{[math]}$ 处与地面 $\text{[math]}$ 的距离为 $\text{[math]}$ 米，车头 $\text{[math]}$ 近似看成一个矩形，且满足 $\text{[math]}$ ，若盲区 $\text{[math]}$ 的长度是 $\text{[math]}$ 米，则车宽 $\text{[math]}$ 的长度为（）米.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2017九上·深圳月考) 墙壁CD上D处有一盏灯（如图），小明站在A站测得他的影长与身长相等都为1.5m，他向墙壁走1m到B处时发现影子刚好落在A点，则灯泡与地面的距离CD=m.

答案解析收藏纠错 + 选题
10. 如图，在测量小玻璃管口径的量具ABC．上，AB的长为14 mm，AC被分为70等份．如果小管口DE正好对着量具40刻度线上处(DE∥AB)，那么小管口径DE的长是mm．

答案解析收藏纠错 + 选题
11. (2024九上·裕华开学考) 如图，小明在 $\text{[math]}$ 时测得某树的影长为 $\text{[math]}$ ， $\text{[math]}$ 时又测得该树的影长为 $\text{[math]}$ ，若两次日照的光线互相垂直，则树的高度为．

答案解析收藏纠错 + 选题
12. 如图所示，放置在水平地面上的一油桶高AC=1m，桶内有油，一根木棒长 $\text{[math]}$ .将木棒从桶盖小口斜插入桶内，一端到桶底 $\text{[math]}$ 处，另一端恰好与桶盖小口 $\text{[math]}$ 处相齐.抽出木棒，若量得棒上的浸油部分DE的长为 $\text{[math]}$ ，则桶内油的深度是 $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2023九上·通川期末) 大约在两千四五百年前，如图1墨子和他的学生做了世界上第1个小孔成倒像的实验．并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”．如图2所示的小孔成像实验中，若物距为10cm，像距为15cm，蜡烛火焰倒立的像的高度是9cm，则蜡烛火焰的高度是 cm．

答案解析收藏纠错 + 选题

三、解答题

14. (2023·锦江模拟) 【学科融合】如图1，在反射现象中，反射光线，入射光线和法线都在同一个平面内：反射光线和入射光线分别位于法线两例；入反射角r等于入射角i.这就是光的反射定律.
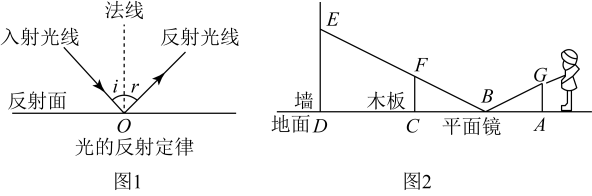
【问题解决】如图2，小红同学正在使用手电筒进行物理光学实验，地面上从左往右依次是墙，木板和平面镜，手电筒的灯泡在点G处，手电筒的光从平面镜上点B处反射后，恰好经过木板的边缘点F，落在墙上的点E处，点E到地面的高度 $\text{[math]}$ ，点F到地面的高度 $\text{[math]}$ ，灯泡到木板的水平距离 $\text{[math]}$ ，木板到墙的水平距离为 $\text{[math]}$ .图中A，B，C，D在同一条直线上.
1. （1）求 $\text{[math]}$ 的长；
2. （2）求灯泡到地面的高度 $\text{[math]}$ .
答案解析收藏纠错 + 选题
15. (2024九上·渠县期末) 如图1，在光的反射现象中，反射光线、入射光线和法线都在同一个平面内，反射光线和入射光线分别位于法线两侧，反射角 $\text{[math]}$ 等于入射角 $\text{[math]}$ ．这就是光的反射定律．
【问题解决】如图2，林舒同学正在使用手电筒进行物理光学实验，地面上从左往右依次是墙，木板和平面镜，手电筒在点 $\text{[math]}$ 处，手电筒的光从平面镜上点 $\text{[math]}$ 处反射后，恰好经过木板的边缘点 $\text{[math]}$ ，落在墙上的点 $\text{[math]}$ 处，点 $\text{[math]}$ 到地面的高度 $\text{[math]}$ ，点 $\text{[math]}$ 到地面的高度 $\text{[math]}$ ，手电筒到木板的水平距离 $\text{[math]}$ ，木板到墙的水平距离为 $\text{[math]}$ ．图中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一条直线上．
1. （1）求 $\text{[math]}$ 的长；
2. （2）求点E到地面的高度 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
16. (2024九上·贵阳期末) 在学习了光的反射定律后，数学综合实践小组想利用光的反射定律（反射角等于入射角）测量池塘对岸一棵树的高度AB ，测量步骤如下：
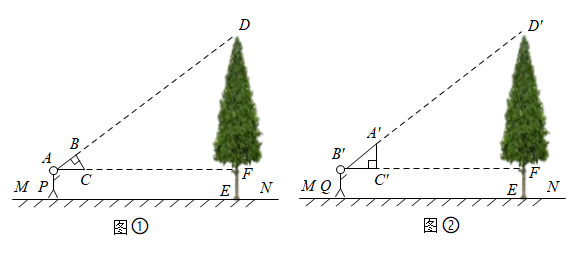
①如图，在地面上的点E处放置一块平面镜（镜子大小忽略不计），小阳站在BE的延长线上，当小阳从平面镜中刚好看到树的顶点A时，测得小阳到平面镜的距离DE＝2m ，小阳的眼睛点C到地面的距离CD＝1.6m；
②将平面镜从点E沿BE的延长线移动6m放置到点H处，小阳从点D处移动到点G ，此时小阳的眼睛点F又刚好在平面镜中看到树的顶点A ，这时测得小阳到平面镜的距离GH＝3.2m ．请根据以上测量过程及数据求出树的高度AB ．

答案解析收藏纠错 + 选题
17. (2024九上·杭州月考) 学习了相似三角形知识后，小丽同学准备用自制的直角三角形纸板测量校园内一颗古树的高度．已知三角形纸板的斜边长为0.5米，较短的直角边长为0.3米．
1. （1）小丽先调整自己的位置至点 $\text{[math]}$ ，将直角三角形纸板的三个顶点位置记为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ （如图①），斜边 $\text{[math]}$ 平行于地面 $\text{[math]}$ （点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在一直线上），且点 $\text{[math]}$ 在边 $\text{[math]}$ （较长直角边）的延长线上，此时测得边 $\text{[math]}$ 距离地面的高度 $\text{[math]}$ 为1.5米，小丽与古树的距离 $\text{[math]}$ 为16米，求古树的高度 $\text{[math]}$ ；
2. （2）为了尝试不同的思路，小丽又向前移动自己的位置至点 $\text{[math]}$ ，将直角三角形纸板的三个顶点的新位置记为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ （如图②），使直角边 $\text{[math]}$ （较短直角边）平行于地面 $\text{[math]}$ （点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在一直线上），点 $\text{[math]}$ 在斜边 $\text{[math]}$ 的延长线上，且测得此时边 $\text{[math]}$ 距离地面的高度依然是1.5米，那么小丽向前移动了多少米？
答案解析收藏纠错 + 选题
18. (2022九上·济南期末) 如图1，长、宽均为3cm，高为8cm的长方体容器，放置在水平桌面上，里面盛有水，水面高为6cm，绕底面一棱进行旋转倾斜后，水面恰好触到容器口边缘，图2是此时的示意图，将这个情景转化成几何图形，如图3所示．
1. （1）利用图1、图2所示水的体积相等，求 $\text{[math]}$ 的长；
2. （2）求水面高度 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2024·吉安模拟) 一块材料的形状是锐角三角形ABC ，下面分别对这块材料进行课题探究：
1. （1）课本再现
  在图1中，若边 $\text{[math]}$ ，高 $\text{[math]}$ ，把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB ， AC上，这个正方形零件的边长是多少?
2. （2）类比探究
  如图2，若这块锐角三角形ABC材料可以加工成3个相同大小的正方形零件，请你探究高AD与边BC的数量关系，并说明理由．
3. （3）拓展延伸
  ①如图3，若这块锐角三角形ABC材料可以加工成图中所示的4个相同大小的正方形零件，则 $\text{[math]}$ 的值为 ▲ （直接写出结果）；
  ②如图4，若这块锐角三角形ABC材料可以加工成图中所示的 $\text{[math]}$ 相同大小的正方形零件，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题