
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
![]()
如图,已知∠AOB,求作:∠DEF,使∠DEF=∠AOB
作法:
(1)以●为圆心,任意长为半径画弧,分别交OA、OB于点P、Q
(2)作射线EG,并以点E为圆心◎长为半径画弧交EG于点D
(3)以点D为圆心⊙长为半径画弧交(2)步中所画弧于点F
(4)作⊕,∠DEF即为所求作的角


 B .
B .  C .
C .  D .
D . 

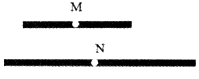
①作出射线;
②在射线上依次截取
;
③在线段上截取
.



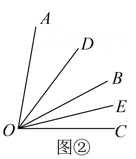
①若 , 射线OC平分
, 射线OE平分
, 求
度数;
②若 , 射线OC平分
, 射线OE平分
, 求
的度数;

未知线段 已知线段 …… | 因为C , D分别是线段 所以
因为 所以 | 线段中点的定义 线段的和、差 等式的性质 |
【问题提出】随着时间的变化,钟面上时针和分针形成夹角的度数也随之变化,记时针和分针的夹角为α(a大于等于 0°,且小于等于 180° ).我们可以求出任意时刻∠α 的度数吗?
分针运动规律 | 分针每分钟走6° | |
时针运动规律 | 时针每小时走30°即每分钟走0.5° | |
规定 | 当时针和分针指向刻度12记为0° | |
特例探究1(8点50分) | 分针绕点O旋转所得角的度数是6°×50=300°,时针绕点O旋转所得角的度数是30°×8+0.5°×50=265°所以∠α=300°-265°=35°. |
|
特例探究2(8时30分) | 分针绕点O旋转所得角的度数是6°×30=180°,时针绕点O旋转所得角的度数是30°×8+0.5°×30=255°所以.∠α=255°-180°=75°. |
|
特例探究3(8时10分) | 分针绕点O旋转形成的角的度数是6°×10=60°,时针绕点O旋转形成的角的度数是30°×8+0.5°×10=245°,此时245°-60°=185°,由于185°>180°,所以∠α=360°-185°=175°. |
|
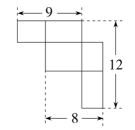
【问题情境】如图,数轴上点A表示的数为﹣2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).

【综合运用】
①A、B两点间的距离AB=,线段AB的中点C表示的数为;
②用含t的代数式表示:t秒后,点P表示的数为;点Q表示的数为;