x | … | -1 | 0 | 1 | 2 | … |
| y | … | m | 2 | 2 | n | … |
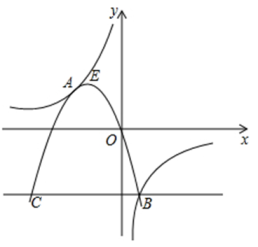
且当时,对应的函数值
有以下结论:
;
;
关于
的方程
的负实数根在
和
之间;
和
在该二次函数的图象上,则当实数
时,
.
其中正确的结论是( )

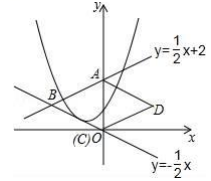


①当△BPM为直角三角形时,求点P的坐标;
②是否存在点P使得PB 与 QN相互平分,若存在,求PQ的长,若不存在,说明理由.

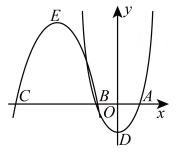
①当点D1刚好落在第二象限的抛物线上时,求出点D的坐标.
②点P在抛物线上(点P不与点A、点C重合),连结PD,PD1 , DD1 , 是否存在点P,使△PDD1为等腰直角三角形?若存在,请求出点P的坐标;若不存在