精选实践探究题—2024年浙教版数学七（上）期中复习

更新时间：2024-10-21 浏览次数：21 类型：复习试卷

一、有理数

1. (2023七上·诸暨期中) 符号“f”表示一种运算，它对一组数的运算如下：
$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ …
1. （1）利用以上运算的规律写出 $\text{[math]}$ ；（ $\text{[math]}$ 为正整数）
2. （2）计算 $\text{[math]}$ ；
3. （3）计算 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
2. (2023七上·温州期中) 根据以下素材，探索完成任务．
素材1：如何规划游玩路线？
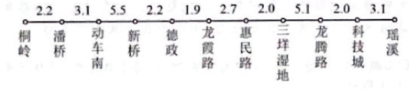
温州轨道交通实行里程分段计价票制，起步价2元，可乘坐4km(含4km)，4至28km(含28km)每1元可乘4km(不足4km按1元算)．如：桐岭站到动车南站共5.3km，收费3元．部分站点距离见下图(单位：km)
素材2：一名成年乘客可免费携带一名身高不足1.2米(含1.2米)的儿童乘车，
素材3：小明一家四口将乘坐轻轨出游．小明家住在新桥站附近，家庭成员如下：小明(身高1.5米)、弟弟(身高1.1米)、爸爸、妈妈．
问题解决
1. （1）任务1
  从新桥站到桐岭站为km，单人单程乘坐需车费元
2. （2）任务2
  小明一家乘坐轻轨从新桥站到三烊湿地站，需要多少车费．
3. （3）任务3
  小明一家从新桥站出发，计划共用30元车费出行(往返)，请你为小明一家规划一个尽可能远的游玩站点，并说明理由．
答案解析收藏纠错 + 选题
3. (2023七上·洞头期中) 素材1：每年秋天是灵昆柿子饼盛产期．小黄同学打算从灵昆寄5袋柿子饼到杭州，以每袋3千克为标准，超过的千克数记为正数，不足的千克数记为负数，记录如下表所示：
柿子饼袋
①
②
③
④
⑤
与标准重量的差值（单位：千克）
0.1
-0.3
0
-0.1
0.2
素材2：小黄同学选择了某快递，收费标准如下：3千克以内15元（含3千克），超过1千克的部分为2元/每千克（不足1千克按1千克计）．现该快递公司提供多种寄件方式：
纸箱类型
中型纸箱
大型纸箱
可容纳袋数（袋/个）
2
4
重量（千克/个）
0.4
0.7
价格（元/个）
3
5
方案一：小黄购买了中型纸箱将重量最低的②、④柿子饼袋打包在一起，其余每小袋各自寄出．
方案二：____．
1. （1）【任务1】求这5袋柿子饼的总重量．
2. （2）【任务2】求方案一所需要的费用．
3. （3）【任务3】请你设计方案二，使它的费用低于方案一，并计算你的方案费用．
答案解析收藏纠错 + 选题
4. (2023七上·温州期中) 根据以下素材，探索完成任务．
如何规划游玩路线？
素材1
温州轨道交通实行里程分段计价票制，起步价2元，可乘坐4km （含4km），4至28km（含28km）每1元可乘4km（不足4km按1元算）．如：桐岭站到动车南站共5.3km，收费3元．部分站点距离见下图（单位：km）
素材2
一名成年乘客可免费携带一名身高不足1.2米（含1.2米）的儿童乘车，
素材3
小明一家四口将乘坐轻轨出游．小明家住在新桥站附近，家庭成员如下：小明（身高1.5米）、弟弟（身高1.1米）、爸爸、妈妈．
问题解决
1. （1）任务1
  从新桥站到桐岭站为km，单人单程乘坐需车费元
2. （2）任务2
  小明一家乘坐轻轨从新桥站到三烊湿地站，需要多少车费．
3. （3）任务3
  小明一家从新桥站出发，计划共用30元车费出行（往返），请你为小明一家规划一个尽可能远的游玩站点，并说明理由．
答案解析收藏纠错 + 选题

5. (2023七上·新昌期中) 根据以下素材，尝试解决问题．

如何获得更高的销售额？

素材 $\text{[math]}$

甲菜农有 $\text{[math]}$ 筐蔬菜，每筐质量在 $\text{[math]}$ 千克左右，超过的千克数记为正数，不足的千克数记为负数，记录如图，超过 $\text{[math]}$ 千克的以 $\text{[math]}$ 元 $\text{[math]}$ 筐的价格售出，其余三筐以 $\text{[math]}$ 元 $\text{[math]}$ 千克销售，全部售出．

素材 $\text{[math]}$

乙菜农将蔬菜堆放在一起进行销售，售出的蔬菜质量比甲菜农少 $\text{[math]}$ 千克，其中 $\text{[math]}$ 千克以 $\text{[math]}$ 元 $\text{[math]}$ 千克销售，剩下的部分按八折全部售出．

问题解决

（1）问题1：求甲菜农售出最重的一筐蔬菜的质量．
（2）问题2：求乙菜农售出的蔬菜的总质量．
（3）问题3：甲、乙菜农的蔬菜全部售出后，比较哪一位菜农的销售额更高，高多少元？

答案解析收藏纠错 + 选题

6. (2022七上·瑞安期中) 国庆期间，某超市各个区域都有促销活动，晓琳一家去逛该超市，准备购买纸巾，根据以下素材，探索完成任务．

揭秘超市促销：送券和打折哪个更优惠
素材1	纸巾区域推出两种活动：活动一：购物满100元送30元券，满200元送60元券，...，上不封顶，送的券当天有效，一次性用完. 活动二：所有商品打8折. 注：两种活动不能同时参加.
素材2	晓琳家用的两种纸巾信息（超市标价）．
素材3	晓琳家平均三天用1包清风牌纸巾，平均五天用1包4D溶纸巾；晓琳家清风牌纸巾还有1袋存货，4D溶纸巾存货不清楚．

问题解决
任务1	半年（按180天计算），试求出需要消耗清风牌纸巾多少袋？消耗4D溶纸巾多少箱？
任务2	按存半年的量计算，还需要购买2种纸巾，其中4D溶纸巾x箱，若选择活动二，则所需的总费用为元（用含x的代数式表示）．
任务3	晓琳突然想起4D溶纸巾没有存货，按半年所需量，请探索送券和打折哪个更优惠？并写出探索过程．

答案解析收藏纠错 + 选题

7. (2023七上·海曙期中) 类比乘方运算，我们规定：求n个相同有理数（均不为0）的商的运算叫做除方.例如 $\text{[math]}$ ，记作 $\text{[math]}$ ，读作“2的引4次商”.一般的，把 $\text{[math]}$ $\text{[math]}$ 记作 $\text{[math]}$ ，读作“a的引n次商”.
1. （1）直接写出计算结果： $\text{[math]}$ =， $\text{[math]}$ =.
2. （2）归纳：负数的引正奇数次商是数，负数的引正偶数次商是数（填“正或负”）；
3. （3）计算： $\text{[math]}$ .
答案解析收藏纠错 + 选题
8. (2023七上·金华期中) 概念学习
规定：求若干个相同的有理数(均不等于0)的除法运算叫做除方，如2÷2÷2，(-3)÷(-3)÷(-3)÷(-3)等．类比有理数的乘方，我们把2÷2÷2记作2^③ ，读作“2的圈3次方”，(-3)÷(-3)÷(-3)÷(-3)记作(-3)^④ ，读作“-3的圈4次方”，一般地，把a÷a÷a÷…÷a ， (n个a ， a≠0)记作，读作“a的圈n次方”．
1. （1）初步探究：
  →2^④=2÷2÷2÷2=2× $\text{[math]}$ × $\text{[math]}$ × $\text{[math]}$ = $\text{[math]}$ →
  ①直接写出计算结果：2^③=， $\text{[math]}$ =；
  ②关于除方，下列说法错误的是
  A．任何非零数的圈2次方都等于1； B．对于任何正整数n ， 1^ⓝ=1；
  C.3^④=4^③ D．负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数．
2. （2）深入思考
  我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢？
  ①试一试：
  仿照上面的算式，将下列运算结果直接写成幂的形式．(-3)^④= ▲ ；5^⑥= ▲ ； $\text{[math]}$ = ▲ ．
  ②想一想：将一个非零有理数a的圈n次方写成幂的形式等于 ▲ ；
  ③算一算：12²÷ $\text{[math]}$ × $\text{[math]}$ - $\text{[math]}$ ÷3³ ．
答案解析收藏纠错 + 选题

二、数轴

9. (2023七上·鄞州月考)
【阅读理解】
点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为数轴上三点，如果点 $\text{[math]}$ 在 $\text{[math]}$ 、 $\text{[math]}$ 之间且到 $\text{[math]}$ 的距离是点 $\text{[math]}$ 到 $\text{[math]}$ 的距离 $\text{[math]}$ 倍，那么我们就称点 $\text{[math]}$ 是 $\text{[math]}$ 的奇点．
例如，如图 $\text{[math]}$ ，点 $\text{[math]}$ 表示的数为 $\text{[math]}$ ，点 $\text{[math]}$ 表示的数为 $\text{[math]}$ 表示 $\text{[math]}$ 的点 $\text{[math]}$ 到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，那么点 $\text{[math]}$ 是 $\text{[math]}$ 的奇点；又如，表示 $\text{[math]}$ 的点 $\text{[math]}$ 到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，那么点 $\text{[math]}$ 就不是 $\text{[math]}$ 的奇点，但点 $\text{[math]}$ 是 $\text{[math]}$ 的奇点．
【知识运用】
如图 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 为数轴上两点，点 $\text{[math]}$ 所表示的数为 $\text{[math]}$ ，点 $\text{[math]}$ 所表示的数为 $\text{[math]}$ ．
1. （1）数所表示的点是 $\text{[math]}$ 的奇点；数所表示的点是 $\text{[math]}$ 的奇点；
2. （2）如图 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 为数轴上两点，点 $\text{[math]}$ 所表示的数为 $\text{[math]}$ ，点 $\text{[math]}$ 所表示的数为 $\text{[math]}$ 现有一动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发向左运动，到达点 $\text{[math]}$ 停止． $\text{[math]}$ 点运动到数轴上的什么位置时， $\text{[math]}$ 、 $\text{[math]}$ 和 $\text{[math]}$ 中恰有一个点为其余两点的奇点？
答案解析收藏纠错 + 选题
10. (2023七上·浙江月考) 阅读理解：
若 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为数轴上三点，若点 $\text{[math]}$ 到 $\text{[math]}$ 的距离是点 $\text{[math]}$ 到 $\text{[math]}$ 的距离 $\text{[math]}$ 倍，我们就称点 $\text{[math]}$ 是【 $\text{[math]}$ ， $\text{[math]}$ 】的好点．
例如，如图 $\text{[math]}$ ，点 $\text{[math]}$ 表示的数为 $\text{[math]}$ ，点 $\text{[math]}$ 表示的数为 $\text{[math]}$ 表示 $\text{[math]}$ 的点 $\text{[math]}$ 到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，那么点 $\text{[math]}$ 是【 $\text{[math]}$ ， $\text{[math]}$ 】的好点；又如，表示 $\text{[math]}$ 的点 $\text{[math]}$ 到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，那么点 $\text{[math]}$ 就不是【 $\text{[math]}$ ， $\text{[math]}$ 】的好点，但点 $\text{[math]}$ 是【 $\text{[math]}$ ， $\text{[math]}$ 】的好点．
知识运用：如图 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 为数轴上两点，点 $\text{[math]}$ 所表示的数为 $\text{[math]}$ ，点 $\text{[math]}$ 所表示的数为 $\text{[math]}$ ．
1. （1）数所表示的点是【 $\text{[math]}$ ， $\text{[math]}$ 】的好点；
2. （2）如图 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 为数轴上两点，点 $\text{[math]}$ 所表示的数为 $\text{[math]}$ ，点 $\text{[math]}$ 所表示的数为 $\text{[math]}$ 现有一只电子蚂蚁 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以 $\text{[math]}$ 个单位每秒的速度向左运动，到达点 $\text{[math]}$ 停止 $\text{[math]}$ 当 $\text{[math]}$ 为何值时， $\text{[math]}$ 、 $\text{[math]}$ 和 $\text{[math]}$ 中恰有一个点为其余两点的好点？
答案解析收藏纠错 + 选题
11. (2023七上·萧山期中) 数轴是一个非常重要的数学工具，它使数和数轴上的点建立起了对应关系，揭示了数与点之间的内在联系
1. （1）操作一：
  折叠纸面，若使1表示的点与-1表示的点重合，则-3表示的点与表示的点重合；
2. （2）操作二：
  折叠纸面，若使1表示的点与3表示的点重合，回答以下问题：
  ①-3表示的点与数表示的点重合；
  ②若数轴上A、B两点之间距离为9（A在B的左侧），且A、B两点经折叠后重合，则A、B两点表示的数分别是，；
3. （3）操作三：
  在数轴上剪下9个单位长度（从-1到8）的一条线段，并把这条线段沿某点折叠（如图所示）．若得到的这三条线段的长度之比为1：1：2，则折痕处对应的点所表示的数可能是多少？
答案解析收藏纠错 + 选题
12. (2023七上·洞头期中) 新定义学习：
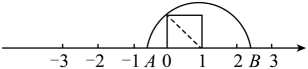
【新知学习】若A，B，C是数轴上的三个点，如果点C到A的距离等于点C到B的距离，那么我们就称点C是AB的中点．例如，如图1，点A表示的数为-1，点B表示的数为3，表示数1的点C到点A的距离是2，到点B的距离是2，那么点C是AB的中点．
1. （1）【知识运用】
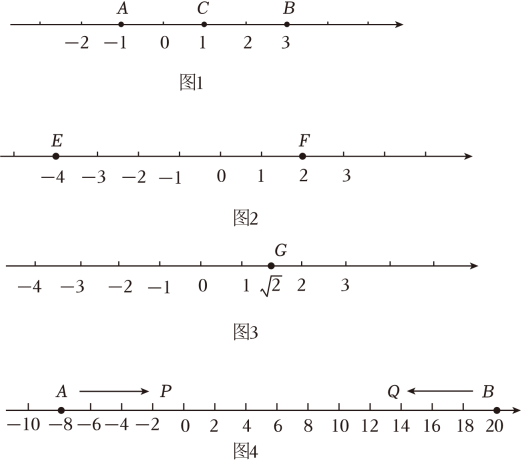
  ①如图2，E、F为数轴上两点，点E所表示的数为-4，点F所表示的数为2，求EF的中点所表示的数，并说明理由．
  ②如图3，若数 $\text{[math]}$ 所表示的点G是MN的中点，那么M表示的数为， N表示的数为（只要写出符合条件的一对值即可）．
2. （2）【知识拓展】如图4，A，B为数轴上两点，点A所表示的数为-8，点B所表示的数为20．现有一只电子蜗牛P从点A出发，以1个单位每秒的速度向右运动；同时另一只电子蜗牛Q从点B出发，以2个单位每秒的速度向左运动，若点M，N分别是AP和BQ的中点，则在P，Q的运动过程中，当t＝秒时，M，N点到原点的距离相等（请直接写出答案）．
答案解析收藏纠错 + 选题
13. (2022七上·杭州期中) 阅读理解：
若 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为数轴上三点，若点 $\text{[math]}$ 到 $\text{[math]}$ 的距离是点 $\text{[math]}$ 到 $\text{[math]}$ 的距离 $\text{[math]}$ 倍，我们就称点 $\text{[math]}$ 是【 $\text{[math]}$ ， $\text{[math]}$ 】的好点．

例如，如图 $\text{[math]}$ ，点 $\text{[math]}$ 表示的数为 $\text{[math]}$ ，点 $\text{[math]}$ 表示的数为 $\text{[math]}$ 表示 $\text{[math]}$ 的点 $\text{[math]}$ 到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，那么点 $\text{[math]}$ 是【 $\text{[math]}$ ， $\text{[math]}$ 】的好点；又如，表示 $\text{[math]}$ 的点 $\text{[math]}$ 到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，到点 $\text{[math]}$ 的距离是 $\text{[math]}$ ，那么点 $\text{[math]}$ 就不是【 $\text{[math]}$ ， $\text{[math]}$ 】的好点，但点 $\text{[math]}$ 是【 $\text{[math]}$ ， $\text{[math]}$ 】的好点．

知识运用：如图 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 为数轴上两点，点 $\text{[math]}$ 所表示的数为 $\text{[math]}$ ，点 $\text{[math]}$ 所表示的数为 $\text{[math]}$ ．
1. （1）数所表示的点是【 $\text{[math]}$ ， $\text{[math]}$ 】的好点；
2. （2）如图 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 为数轴上两点，点 $\text{[math]}$ 所表示的数为 $\text{[math]}$ ，点 $\text{[math]}$ 所表示的数为 $\text{[math]}$ 现有一只电子蚂蚁 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以 $\text{[math]}$ 个单位每秒的速度向左运动，到达点 $\text{[math]}$ 停止 $\text{[math]}$ 当 $\text{[math]}$ 为何值时， $\text{[math]}$ 、 $\text{[math]}$ 和 $\text{[math]}$ 中恰有一个点为其余两点的好点？
答案解析收藏纠错 + 选题
14. (2022七上·杭州月考) 【方法感悟】阅读下面材料：
点A，B在数轴上分别表示实数a，b，A，B两点之间的距离表示为 $\text{[math]}$ .如图1，从数轴上看，若点A，B表示的分别是1，4则 $\text{[math]}$ 或 $\text{[math]}$ ；

若点A，B表示的数分别是 $\text{[math]}$ ， 4则 $\text{[math]}$ 或 $\text{[math]}$ ；

若点A，B表示的数分别是 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 或 $\text{[math]}$ ．

【归纳】若点A，B表示的数分别是 $\text{[math]}$ ， $\text{[math]}$ 则 $\text{[math]}$ 或 $\text{[math]}$ ．

【知识迁移】
1. （1）如图1，点A，B表示的数分别是 $\text{[math]}$ ， b且 $\text{[math]}$ ，则 $\text{[math]}$ ；
2. （2）如图2，点A，B表示的数分别是 $\text{[math]}$ ， $\text{[math]}$ ，若把 $\text{[math]}$ 向左平移 $\text{[math]}$ 个单位，则点A与 $\text{[math]}$ 重合，若把 $\text{[math]}$ 向右平移 $\text{[math]}$ 个单位，则点B与70重合，那么 $\text{[math]}$ ， $\text{[math]}$ ；
3. （3）【拓展应用】
  一天，美羊羊去问村长爷爷的年龄，村长爷爷说：“我若是你现在这么大，你还要40年才出生呢，你若是我现在这么大，我已经是老寿星了，116岁了，哈哈！”美羊羊纳闷，请问村长爷爷现在到底是多少岁？美羊羊现在又是几岁？请写出解题思路.
4. （4）结合几何意义，求 $\text{[math]}$ 最小值.
答案解析收藏纠错 + 选题

三、实数

15. (2023七上·余姚期中) 教材上有这样一个合作学习活动：如图1，依次连结2×2方格四条边的中点A ， B ， C ， D ，得到一个阴影正方形．设每一小方格的边长为1，得到阴影正方形面积为2．
1. （1）【基础尝试】：
  发现图1这个阴影正方形的边长就是小方格的对角线长，则小方格对角线长是，由此我们得到一种在数轴上找到无理数的方法；
2. （2）【画图探究】：
  如图2，以1个单位长度为边长画一个正方形，以数字1所在的点为圆心，正方形的对角线为半径画弧，与数轴交于M ， N两点，则点M表示的数为；
3. （3）【问题解决】：
  如图3，3×3网格是由9个边长为1的小方格组成．
  ①画出面积是5的正方形，使它的顶点在网络的格点上；
  ②请借鉴（2）中的方法在数轴上找到表示实数 $\text{[math]}$ 的准确位置．（保留作图痕迹并标出必要线段长）
答案解析收藏纠错 + 选题
16. (2023七上·杭州月考) 如图①，把两个边长为 $\text{[math]}$ 的小正方形沿对角线剪开，所得的 $\text{[math]}$ 个直角三角形拼成一个面积为 $\text{[math]}$ 的大正方形．由此得到了一种能在数轴上画出无理数对应点的方法．
1. （1）图②中 $\text{[math]}$ 、 $\text{[math]}$ 两点表示的数分别为，；
2. （2）请你参照上面的方法：
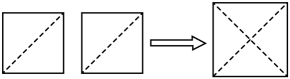
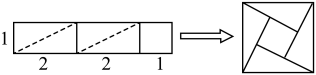
  把图③中 $\text{[math]}$ 的长方形进行剪裁，并拼成一个大正方形．在图③中画出裁剪线，并在图④的正方形网格中画出拼成的大正方形，该正方形的边长 $\text{[math]}$ ▲ ．（注：小正方形边长都为 $\text{[math]}$ ，拼接不重叠也无空隙）
答案解析收藏纠错 + 选题
17. (2023七上·期中) 如图，有这样一个探究：把两个边长为1的小正方形分别沿对角线剪开，将所得的4个直角三角形拼在一起，可以得到一个面积为2的大正方形，试根据这个研究方法回答下列问题：
1. （1）所得到的面积为2的大正方形的边长就是原边长为1的小正方形的对角线长，因此可得小正方形的对角线长为；
2. （2）由此我们得到一种在数轴上找到无理数的方法：如下图，以单位长度为边长画一个正方形，以数字1所在的点为圆心，正方形的对角线为半径画弧，与数轴交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，那么 $\text{[math]}$ 点表示的数为；
3. （3）通过动手操作，漠子同学把长为5，宽为1的长方形进行裁剪，拼成如图所示的正方形．请借鉴（2）中的方法在数轴上找到表示 $\text{[math]}$ 的点 $\text{[math]}$ ．（保留作图痕迹并标出必要线段长）
答案解析收藏纠错 + 选题
18. (2023七上·义乌期中) 阅读下列信息材料：
信息1：因为无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来比如：π、 $\text{[math]}$ 等，而常用的“…”或者“≈”的表示方法都不够百分百准确；
信息2：2.5的整数部分是2，小数部分是0.5，可以看成2.5﹣2得来的；
信息3：任何一个无理数，都可以夹在两个相邻的整数之间，如2＜ $\text{[math]}$ ＜3，是因为 $\text{[math]}$ ；
根据上述信息，回答下列问题：
1. （1） $\text{[math]}$ 的整数部分是，小数部分是；
2. （2） 8+ $\text{[math]}$ 也是夹在相邻两个整数之间的，可以表示为a＜8+ $\text{[math]}$ ＜b则a+b＝；
3. （3）若 $\text{[math]}$ －2＝a+b，其中a是整数，且0＜b＜1，请求2a-b的相反数．
答案解析收藏纠错 + 选题
19. (2023七上·余姚期中) 教材上有这样一个合作学习活动：如图1，依次连结2×2方格四条边的中点A ， B ， C ， D ，得到一个阴影正方形．设每一小方格的边长为1，得到阴影正方形面积为2．
1. （1）【基础尝试】
  发现图1这个阴影正方形的边长就是小方格的对角线长，则小方格对角线长是，由此我们得到一种在数轴上找到无理数的方法；
2. （2）【画图探究】
  如图2，以1个单位长度为边长画一个正方形，以数字1所在的点为圆心，正方形的对角线为半径画弧，与数轴交于M ， N两点，则点M表示的数为；
3. （3）【问题解决】
  如图3，3×3网格是由9个边长为1的小方格组成．
  ①画出面积是5的正方形，使它的顶点在网络的格点上；
  ②请借鉴（2）中的方法在数轴上找到表示实数 $\text{[math]}$ 的准确位置．(保留作图痕迹并标出必要线段长)
答案解析收藏纠错 + 选题

四、一元一次方程

20. (2023七上·椒江月考) 请阅读下列材料，并完成相应任务．

如图1，公元前300年前后，欧几里得撰写的《几何原本》系统地论述了黄金分割，称为最早的有关黄金分割的论著．黄金分割是指把一条线段分割成两部分，使较大部分与全长的比值等于较小部分与较大部分的比值．如图2，在线段 $\text{[math]}$ 上找一点 $\text{[math]}$ ，把线段 $\text{[math]}$ 分成 $\text{[math]}$ 和 $\text{[math]}$ 两段，其中 $\text{[math]}$ 是较短的一段．如果 $\text{[math]}$ ，那么称线段 $\text{[math]}$ 被点 $\text{[math]}$ 黄金分割， $\text{[math]}$ 叫做线段 $\text{[math]}$ 的黄金分割点，这个比值叫做黄金分割数，约为 $\text{[math]}$ ，即 $\text{[math]}$ ， $\text{[math]}$ ．

完成以下任务：

（1）如图2，线段 $\text{[math]}$ 被点 $\text{[math]}$ 黄金分割．若 $\text{[math]}$ 长为 $\text{[math]}$ ，求 $\text{[math]}$ 的长；（结果保留小数点后一位）
（2）如图3，一根一侧烧毁的木棒工件 $\text{[math]}$ （粗度不计），在它的两个黄金分割点 $\text{[math]}$ ， $\text{[math]}$ 处钻有小孔．若量得 $\text{[math]}$ ， $\text{[math]}$ 间的距离约为 $\text{[math]}$ ，求木棒 $\text{[math]}$ 的原长度．

答案解析收藏纠错 + 选题

21. (2024七上·柯桥期中) 每年“双十一”购物节，商家都会利用这个契机进行促销活动.今年某超市也有促销活动，小明一家去逛该超市，准备购买纸巾，根据以下素材，探索完成任务．
素材1   纸巾区域推出两种活动：活动一：购物满100元送25元券，满200元送50元券，满300元送75元券，…，上不封顶，送的券当天有效，一次性用完．
活动二：所有商品打8.5折．（注：两种活动不能同时参加）
素材2   小明家用的两种纸巾信息（超市标价）
素材3   小明家平时同时使用这两种纸巾，平均三天用1包清风牌纸巾，平均五天用1包4D溶纸巾；小明家清风牌纸巾还有1袋存货，4D溶纸巾存货不清楚.
1. （1）任务1 半年（按180天计算），试求出需要消耗清风牌纸巾多少袋？消耗4D溶纸巾多少箱？
2. （2）任务2 按存半年的量计算，还需要购买2种纸巾，其中4D溶纸巾x箱，若选择活动二，则所需的总费用为元（用含x的代数式表示）；
3. （3）任务3 小明突然想起4D溶纸巾没有存货，按半年所需量，请探索送券和打折哪个更优惠？并写出探索过程.
答案解析收藏纠错 + 选题

22. (2023七上·瑞安期中)

怎么做出更多的纸盒
素材1	如右图，用4个长方形纸板作侧面，1个正方形纸板作底面可以做成1个竖式无盖纸盒
素材2	如右图，用2个长方形纸板与2个正方形纸板作侧面，1个长方形纸板作底面可以做成1横式无盖纸盒
素材3	现有200张长方形纸板与100张正方形纸板

问题解决

（1）问题1 若要使做成的竖式无盖纸盒与横式无盖纸盒的数量一样多，则最多可以做成多少个无盖纸盒（两种纸盒之和）？
（2）问题2 若要使做成的竖式无盖纸盒比横式无盖纸盒多10个，则最多可以做成多少个无盖纸盒（两种纸盒之和）？
（3）问题3 若要先做出10个竖式无盖纸盒，接着再做竖式无盖纸盒或横式无盖纸盒，则最后最多可以做成个无盖纸盒（两种纸盒之和，包括先做出的10个纸盒）？(直接写答案)

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

精选实践探究题—2024年浙教版数学七（上）期中复习

副标题：

*注意事项：

精选实践探究题—2024年浙教版数学七（上）期中复习

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

柿子饼袋	①	②	③	④	⑤
与标准重量的差值（单位：千克）	0.1	-0.3	0	-0.1	0.2

纸箱类型	中型纸箱	大型纸箱
可容纳袋数（袋/个）	2	4
重量（千克/个）	0.4	0.7
价格（元/个）	3	5