浙教版数学七上考点突破训练：有理数的乘除运算

更新时间：2024-10-26 浏览次数：4 类型：复习试卷

一、有理数的乘法运算

1. (2024七上·上城期末) 四个互不相等的整数的积为49，则它们的和为（）

A . 0 B . 8 C . 16 D . 8或1

答案解析收藏纠错 + 选题
2. (2024七上·顺庆月考) 7个有理数相乘的积是负数，那么其中负因数的个数最多有（）

A . $\text{[math]}$ 种可能 B . $\text{[math]}$ 种可能 C . $\text{[math]}$ 种可能 D . $\text{[math]}$ 种可能

答案解析收藏纠错 + 选题
3. (2023七上·鄞州月考) 法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”是一样的，后面的就改用手势了．下面两个图框是用法国“小九九”计算 $\text{[math]}$ 和 $\text{[math]}$ 的两个示例．若用法国的“小九九”计算 $\text{[math]}$ ，左、右手依次伸出手指的个数是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022七上·永嘉期中) 如图，碳足迹标签是一种让大众了解某一产品或服务所产生的碳排放量的标示方式．规定一定条件下碳足迹数据的标示为距离碳排放量最近的一个偶数，例如，碳排放量为20.2克，碳足迹数据标示为20克；碳排放量为21.0克，碳足迹数据标示为20克或22克；碳排放量为21.6克，碳足迹数据标示为22克．已知一个产品的碳足迹数据标示为32克，若此产品的碳排放量减少为原来的80%，则此时该产品碳足迹数据的标示是（）

A . 26克 B . 24克或26克 C . 25克或26克 D . 24克或25

答案解析收藏纠错 + 选题
5. 已知a,b的和，a,b的积及b的相反数均为负，则a,b,-a,a+b,b-a的大小关系是．（用“<”把它们连接起来）

答案解析收藏纠错 + 选题
6. (2023七上·越城月考) 下列说法：①若ab＞0，则a＞0，b＞0；②若ab＜0，则a＜0，b＜0；③若ab＝0，则a或b至少有一个为0；④若ab＞0，且a＋b＜0，则a＜0，b＜0.其中正确的有.

答案解析收藏纠错 + 选题
7. (2023七上·鄞州月考) 数学活动课上，王老师在 $\text{[math]}$ 张卡片上写了 $\text{[math]}$ 个不同的数：
如果从中任意抽取 $\text{[math]}$ 张，使这 $\text{[math]}$ 张卡片上的数之积最小，最小的积为；使这 $\text{[math]}$ 张卡片上的数字之积最大，最大的积为．

答案解析收藏纠错 + 选题
8. (2024七上·南浔期末) “格子乘法”作为两个数相乘的一种计算方法最早在15世纪由意大利数学家帕乔利提出，在明代的《算法统宗》一书中被称为“铺地锦”，如图1，计算47×51，将乘数47计入上行，乘数51计入右行，然后以乘数47的每位数字乘以乘数51的每位数字，将结果计入相应的格子中，最后按斜行加起来（斜行的和均小于10），得2397．如图2，用“铺地锦”的方法表示两个两位数相乘，这两个两位数相乘的结果为．

答案解析收藏纠错 + 选题
9.
1. （1）计算：
  $\text{[math]}$
2. （2）计算： $\text{[math]}$ ×(-9)．下面是两位同学的解法：
  小方：原式= $\text{[math]}$ ×9= $\text{[math]}$ = $\text{[math]}$
  小杨：原式=(19+ $\text{[math]}$ ×(-9)=-19×9- $\text{[math]}$ ×9= $\text{[math]}$
  ①两位同学的解法中，谁的解法较好？
  ②请你写出另一种更好的解法．
答案解析收藏纠错 + 选题
10. (2023七上·鄞州月考) 在学习有理数的乘法时，李老师和同学们做了这样一个游戏：将 $\text{[math]}$ 这个数说给第一名同学，第一名同学将它减去它的 $\text{[math]}$ 的结果告诉第二名同学，第二名同学再将听到的结果减去它的 $\text{[math]}$ 的结果告诉第三名同学，第三名同学再将听到的结果减去它的 $\text{[math]}$ 的结果告诉第四名同学， $\text{[math]}$ 照这样的方法直到全班 $\text{[math]}$ 名同学全部传完，最后一名同学将听到的结果告诉李老师 $\text{[math]}$ 你知道最后的结果吗？

答案解析收藏纠错 + 选题

二、有理数的除法运算

11. (2024七上·玉林期中) 已知 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 0 B . $\text{[math]}$ 或1 C . 2或 $\text{[math]}$ D . 0或 $\text{[math]}$

答案解析收藏纠错 + 选题
12. 若a+b＜0，且 $\text{[math]}$ ＜0，则（　　）

A . a，b异号且负数的绝对值大 B . a，b异号且正数的绝对值大 C . a＞0，b＞0 D . a＜0，b＜0

答案解析收藏纠错 + 选题
13. 已知：ab≠0，且M= $\text{[math]}$ ，当a、b取不同的值时，M有（　　）

A . 唯一确定的值 B . 2种不同的取值 C . 3种不同的取值 D . 4种不同的取值

答案解析收藏纠错 + 选题
14. 下列计算正确的是（）

A . 0÷(-3)= $\text{[math]}$ B . ( $\text{[math]}$ )÷( $\text{[math]}$ )=-5 C . 1÷( $\text{[math]}$ )=-9 D . $\text{[math]}$ ÷(-3)=- 9

答案解析收藏纠错 + 选题
15. (2024七上·新宁期末) 已知a，b是有理数，若a在数轴上的对应点的位置如图所示， $\text{[math]}$ ，有以下结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ，则所有正确的结论是（）

A . ①④ B . ①③ C . ②③ D . ②④

答案解析收藏纠错 + 选题
16. (2023七上·鄞州月考) 定义： $\text{[math]}$ 是不为 $\text{[math]}$ 的有理数，我们把 $\text{[math]}$ 称为 $\text{[math]}$ 的差倒数 $\text{[math]}$ 如： $\text{[math]}$ 的差倒数是 $\text{[math]}$ ， $\text{[math]}$ 的差倒数是 $\text{[math]}$ 已知 $\text{[math]}$ 是 $\text{[math]}$ 的差倒数， $\text{[math]}$ 是 $\text{[math]}$ 的差倒数， $\text{[math]}$ 是 $\text{[math]}$ 的差倒数， $\text{[math]}$ ，以此类推，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2024七上·北京市月考) 如图所示，在数轴上有 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三个点，请回答下列问题：
1. （1）若将点 $\text{[math]}$ 沿数轴向左移动 $\text{[math]}$ 个单位长度，则 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三个点所表示的数谁最小？
2. （2）移动 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三个点中的两个点，使三个点所表示的数相同？请你描述一种移动方法；
3. （3）若将数轴折叠，使得 $\text{[math]}$ 点与表示 $\text{[math]}$ 的点重合， $\text{[math]}$ 点与点 $\text{[math]}$ 重合，则点 $\text{[math]}$ 表示的数是；
4. （4）若数轴上 $\text{[math]}$ 、 $\text{[math]}$ 两点之间的距离为 $\text{[math]}$ （ $\text{[math]}$ 在 $\text{[math]}$ 的左侧），且 $\text{[math]}$ 、 $\text{[math]}$ 两点经过（3）中折叠后互相重合，则 $\text{[math]}$ 点表示的数是， $\text{[math]}$ 点表示的数是．
答案解析收藏纠错 + 选题
18. (2023七上·南昌月考) 请你先认真阅读材料：
计算 $\text{[math]}$

解：原式的倒数是 $\text{[math]}$

＝ $\text{[math]}$

＝ $\text{[math]}$ ×（﹣30）﹣ $\text{[math]}$ ×（﹣30）+ $\text{[math]}$ ×（﹣30）﹣ $\text{[math]}$ ×（﹣30）

＝﹣20﹣（﹣3）+（﹣5）﹣（﹣12）

＝﹣20+3﹣5+12

＝﹣10

故原式等于﹣ $\text{[math]}$

再根据你对所提供材料的理解，选择合适的方法计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2023七上·通川期末) （概念学习）规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如 $\text{[math]}$ ， $\text{[math]}$ 等.类比有理数的乘方，我们把 $\text{[math]}$ 记作 $\text{[math]}$ ，读作“2的圈3次方”， $\text{[math]}$ 记作 $\text{[math]}$ ，读作“ $\text{[math]}$ 的圈4次方”，一般地，把 $\text{[math]}$ 记作，读作“a的圈n次方”.
1. （1）直接写出计算结果： $\text{[math]}$ ， $\text{[math]}$ .
2. （2）（深入思考）我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘法运算此处不用作答）
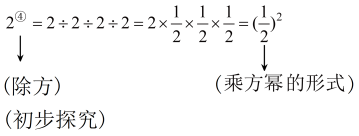
  试一试：仿照上面的算式，将下列运算结果直接写成幂的形式 $\text{[math]}$ ； $\text{[math]}$ .
3. （3）算一算： $\text{[math]}$ .
答案解析收藏纠错 + 选题
20. 一粒米微不足道，平时总会在饭桌上毫不经意地掉下几粒，甚至有些挑食的同学会把整碗米饭倒掉．针对这种浪费粮食现象，老师组织同学们进行了实际测算，称得500粒大米约重10克．现在请你来计算：
1. （1）一粒大米重约多少克？
2. （2）按14亿人口，每年365天，每人每天三餐计算，若每人每餐节约一粒大米，一年大约能节约大米多少千克？（用科学记数法表示）；
3. （3）若我们把一年节约的大米卖成钱，按4元/千克计算，可卖得人民币多少元？（用科学记数法表示）；
4. （4）经过以上计算，你有何感想和建议？
答案解析收藏纠错 + 选题

三、有理数的乘除混合运算

21. (2024七上·新安期末) 我们把2÷2÷2记作2^③ ，（﹣4）÷（﹣4）记作（﹣4）^② ，那么计算9×（﹣3）^④的结果为（）

A . 1 B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
22. (2024七上·益阳开学考) 若“！”是一种数学运算符号，并且1!=1， 2!=2 $\text{[math]}$ 1=2， 3!=3 $\text{[math]}$ 2 $\text{[math]}$ 1=6，……，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . 99！ C . 9900 D . 2！

答案解析收藏纠错 + 选题
23. (2023七上·杭州月考) 下列变形不正确的是（）

A . 5×(－6)＝(－6)×5 B . [4×(－5)] ×(－10)＝4×[ (－5)×(－10) ] C . [(－ $\text{[math]}$ )＋ $\text{[math]}$ ]×(－12)＝(－ $\text{[math]}$ )×(－12) ＋ $\text{[math]}$ ×(－12) D . (－8)× $\text{[math]}$ ×(－1)× $\text{[math]}$ ＝(－8× $\text{[math]}$ ×1× $\text{[math]}$ )

答案解析收藏纠错 + 选题
24. (2023七上·台江开学考) 下列哪一幅图的规律和其他图不一样？（）

A . B . C . D .

答案解析收藏纠错 + 选题
25. (2024七上·新都开学考) 在直径为8分米的圆形钢板上截取一个最大的正方形，这个正方形的面积是平方分米．

答案解析收藏纠错 + 选题
26. 两根细木条，一根长80厘米，另一根长130厘米，将它们其中的一端重合，放在同一条直线上，此时两根细木条的中点间的距离是．

答案解析收藏纠错 + 选题
27. (2023七上·和平期中) 如下图所示，对于任意正整数，若 $\text{[math]}$ 为奇数则乘3再加1，若 $\text{[math]}$ 为偶数则除以2，在这样一次变化下，我们得到一个新的自然数．在1937年 $\text{[math]}$ 提出了一个问题：如此反复这种变换，是否对于所有的正整数，最终都能变换到1呢？这就是数学中著名的“考拉兹猜想”．如果某个正整数通过上述变换能变成1，我们就把第一次变成1时所经过的变换次数称为它的路径长，例如5经过5次变成1，则路径长 $\text{[math]}$ ．若输入数 $\text{[math]}$ ，路径长为 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 的所有可能值有个，其中最小值为．

答案解析收藏纠错 + 选题
28. (2023七上·北京市期中) 北京的水资源非常匮乏，为促进市民节水，从2014年5月1日起北京市居民用水实行阶梯水价，实施细则如下表：
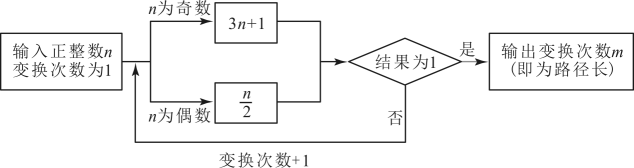
北京市居民用水阶梯水价表
某户居民从2015年1月1日至4月30日，累积用水200立方米，则这户居民4个月共需缴纳水费元．

答案解析收藏纠错 + 选题
29. 阅读后回答问题：
计算（﹣ $\text{[math]}$ ）÷（﹣15）×（﹣ $\text{[math]}$ ）
解：原式=﹣ $\text{[math]}$ ÷[（﹣15）×（﹣ $\text{[math]}$ ）]①
=﹣ $\text{[math]}$ ÷1②
=﹣ $\text{[math]}$ ③
1. （1）上述的解法是否正确？答：
  若有错误，在哪一步？答：（填代号）
  错误的原因是：
2. （2）这个计算题的正确答案应该是：．
答案解析收藏纠错 + 选题
30. (2024七上·长沙期末) 上午9点，我海军驱逐舰发现有不明舰艇在我国专属经济区内活动，我军驱逐舰立即以每小时35海里的速度前往识别．上午9点30分发现不明舰艇为某国舰艇在从事非法活动，于是立即发出驱离警告，此时某国舰艇距我海军驱逐舰11海里并开始逃跑，逃跑的速度是每小时25海里，我海军驱逐舰仍以原来的速度紧追．在距某国舰艇1海里的时候第二次发出驱离警告，90分钟后某国舰艇驶出了我国专属经济区．
1. （1）我海军驱逐舰从发现不明舰艇到第一次发出驱离警告，航行了多少海里？
2. （2）某国舰艇从逃跑至驶出我国专属经济区共经历了多长时间？
3. （3）我海军驱逐舰从发现不明舰艇到第二次发出驱离警告共航行了多少海里？
答案解析收藏纠错 + 选题