


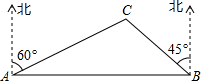
(1)如图1,若 , 求b的值;
(2)某公园准备在园内一个锐角三角形水池中建一座小型景观桥
(如图2所示),若
米,
米,
, 求景观桥
的长度.
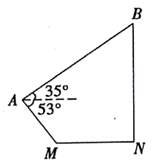
53°,这架无人机沿仰角为350的方向飞行了56米到达点B,恰好在地面上点N的正
上方,M,N在同一水平线上.求M,N两点之间的距离. (结果精确到1米.参考数据: sin53°≈0.80 ,cos53°≈0.60,tan53°≈1 .33, sin35°≈0.57,cos35°≈0.82,
tan35°≈0.70 )



(问题背景)如图1,在△ABC中,点D在边BC上且满足∠BAD=∠ACB,求证:BA2=BD•BC;
(尝试应用)如图2,在△ABC中,点D在边BC上且满足∠BAD=∠ACB,点E在边AB上,点G在AB的延长线上,延长ED交CG于点F,若3AD=2AC,BE=ED,BG=2,DF=1,求BE的长度;
(拓展创新)如图3,在△ABC中,点D在边BC上(AB≠AD)且满足∠ACB=2∠BAD,DH⊥AB垂足为H,若 ,请直接写出
的值 ▲ .

【实践工具】皮尺、测角仪等测量工具
【实践活动】某班甲小组根据胡岸地形状况,在岸边选取合适的点B . 测量A , B两点间的距离以及∠PAB和∠PBA , 测量三次取平均值,得到数据:AB=60米,∠PAB=79°,∠PBA=64°.画出示意图,如图1:

(参考数据:sin64°≈0.90,sin79°≈0.98,cos79°≈0.19,sin37°≈0.60,tan37°≈0.75)
如图2,选择合适的点D , E , F , 使得A , D , E在同一条直线上,且AD=DE , ∠DEF=∠DAP , 当F , D , P在同一条直线上时,只需测量EF即可.
乙小组的方案用到了 .(填写正确答案的序号)
①解直角三角形
②三角形全等
【教师评价】甲、乙两小组的方案都很好,对于实际测量,要根据现场地形状况选择可实施的方案.