解直角三角形之母子模型—浙教版数学九（下）知识点训练

更新时间：2024-12-01 浏览次数：7 类型：复习试卷

一、单选题

1. (2022·广阳模拟) 如图，胡同左右两侧是竖直的墙，一架 $\text{[math]}$ 米长的梯子BC斜靠在右侧墙壁上，测得梯子与地面的夹角为45°，此时梯子顶端B恰巧与墙壁顶端重合．因梯子阻碍交通，故将梯子底端向右移动一段距离到达D处，此时测得梯子AD与地面的夹角为60°，则胡同左侧的通道拓宽了（）

A . $\text{[math]}$ 米 B . 3米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

答案解析收藏纠错 + 选题
2. (2021九上·长清期末) 如图，在A处测得点P在北偏东60°方向上，在B处测得点P在北偏东30°方向上，若AB=2米，则点P到直线AB距离PC为（）

A . 3米 B . $\text{[math]}$ 米 C . 2米 D . 1米

答案解析收藏纠错 + 选题
3. (2020·重庆模拟) 一天，小战和同学们一起到操场测量学校旗杆高度，他们首先在斜坡底部C地测得旗杆顶部A的仰角为45°，然后上到斜坡顶部D点处再测得旗杆顶部A点仰角为37°（身高忽略不计）.已知斜坡CD坡度i=1：2.4，坡长为2.6米，旗杆AB所在旗台高度EF为1.4米，旗台底部、台阶底部、操场在同一水平面上.则请问旗杆自身高度AB为（　　）米.
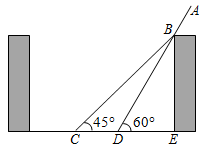
（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）

A . 10.2 B . 9.8 C . 11.2 D . 10.8

答案解析收藏纠错 + 选题
4. (2023·房县模拟) 如图，为了测得电视塔的高度AB，在D处用高为1米的测角仪CD，测得电视塔顶端A的仰角为30°，再向电视塔方向前进100米到达F处，又测得电视塔顶端A的仰角为60°，则这个电视塔的高度AB（单位：米）为（）．

A . $\text{[math]}$ B . 51 C . $\text{[math]}$ D . 101

答案解析收藏纠错 + 选题

二、填空题

5. 在一次综合实践活动中，某学校数学兴趣小组对一电视发射塔的高度进行了测量．如图，在塔前C处，测得该塔顶端B的仰角为 $\text{[math]}$ ，后退 $\text{[math]}$ （ $\text{[math]}$ ）到D处有一平台，在高 $\text{[math]}$ （ $\text{[math]}$ ）的平台上的E处，测得B的仰角为 $\text{[math]}$ ．则该电视发射塔的高度 $\text{[math]}$ 为 $\text{[math]}$ ．（精确到 $\text{[math]}$ ．参考数据： $\text{[math]}$ ）

答案解析收藏纠错 + 选题

三、解答题

6. (2024·娄底模拟) 如图，一枚运载火箭从地面O处发射，当火箭到达点A处时．地面R处的雷达站测得AR的距离是4 km，仰角为30°．经过5 s后，火箭直线上升到达点B处，此时地面R处的雷达站测得B处的仰角为45°．求火箭从A到B处的平均速度（结果精确到1 m/s，参考数据： $\text{[math]}$ ， $\text{[math]}$ ）．

答案解析收藏纠错 + 选题
7. 如图，在电线杆上的C处引拉线CE，CF固定电线杆，拉线CE和地面成60°角，在离电线杆6米的B处安置测角仪，在A处测得电线杆上C处的仰角为30°，已知测角仪高AB为1.5米，求拉线CE的长.(结果保留根号)

答案解析收藏纠错 + 选题
8. (2019九下·建湖期中) 金桥学校“科技体艺节”期间，八年级数学活动小组的任务是测量学校旗杆AB的高.他们在旗杆正前方台阶上的点C处，测得旗杆顶端A的仰角为45°，朝着旗杆的方向走到台阶下的点F处，测得旗杆顶端的仰角为60°.已知升旗台的高度BE为1米，点距地面的高度CD为3米，台阶CF的坡角为30°，且点E，F，D在同一条直线上.求旗杆AB的高.（计算结果精确到0.1米，参考数据： $\text{[math]}$ ）

答案解析收藏纠错 + 选题
9. (2020·昌吉模拟) 某市地铁工程正在加快建设，为了缓解市区内一些主要路段交通拥挤的现状，交警大队在一些主要路口设立了交通路况指示牌，如图所示，小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和30°.求路况指示牌DE的高度.（精确到0.01米，参考数据： $\text{[math]}$ ≈1.732，sin52°≈0.79，cos52°≈0.62， tan52°≈1.28.）

答案解析收藏纠错 + 选题
10. (2020九上·青神期中) 如图，在一次数学课外实践活动中，要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD ，测得教学楼顶端A的仰角为30°，然后向教学楼前进40m到达E ，又测得教学楼顶端A的仰角为60°．求这幢教学楼的高度AB ．（结果带根号）

答案解析收藏纠错 + 选题
11. (2018·正阳模拟) 位于河南省郑州市的炎黄二帝巨型塑像，是为代表中华民族之创始、之和谐、之统一．塑像由山体CD和头像AD两部分组成．某数学兴趣小组在塑像前50米处的B处测得山体D处的仰角为45°，头像A处的仰角为70.5°，求头像AD的高度．（最后结果精确到0.1米，参考数据：sin70.5°≈0.943，cos70.5°≈0.334，tan70.5°≈2.824）

答案解析收藏纠错 + 选题
12. (2024·杭州二模) 《海岛算经》是中国古代测量术的代表作，原名《重差》．这本著作建立起了从直接测量向间接测量的桥梁．直至近代，重差测量法仍有借鉴意义．
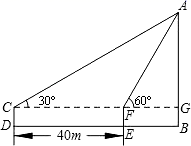
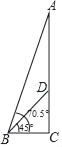
如图2，为测量海岛上一座小山峰AH的高度，在水平地面上直立两根高2米的标杆BC和DE ，两杆间距BD相距6米，D、B、H三点共线．从点B处退行到点F ，观察小山顶A ，发现A、C、F三点共线，且仰角为45°；从点D处退行到点G ，观察小山顶A ，发现A、E、G三点共线，且仰角为30°．（点F、G都在直线HB上）
1. （1）求FG的长（结果保留根号）；
2. （2）小山峰高度AH的长（结果精确到0.1米）．（参考数据： $\text{[math]}$ ≈1.41， $\text{[math]}$ ≈1.73）
答案解析收藏纠错 + 选题
13. (2023·江北模拟) 由于发生山体滑坡灾害，武警救援队火速赶往灾区救援，探测出某建筑物废下方点C处有生命迹象，在废墟一侧地面上探测点A、B相距2米，探测线与该地面的夹角分别是30°和60°（如图所示），试确定生命所在点C的深度.（参考数据： $\text{[math]}$ ≈1.414， $\text{[math]}$ ≈1.732，结果精确到0.1）

答案解析收藏纠错 + 选题
14. (2022·薛城模拟) 位于河南省登封市境内的元代观星台，是中国现存最早的天文台，也是世界文化遗产之一.

某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示，他们在地面一条水平步道 $\text{[math]}$ 上架设测角仪，先在点M处测得观星台最高点A的仰角为 $\text{[math]}$ ，然后沿 $\text{[math]}$ 方向前进 $\text{[math]}$ 到达点N处，测得点 $\text{[math]}$ 的仰角为 $\text{[math]}$ .测角仪的高度为 $\text{[math]}$ ，
1. （1）求观星台最高点A距离地面的高度(结果精确到 $\text{[math]}$ .参考数据： $\text{[math]}$ )；
2. （2） “景点简介”显示，观星台的高度为 $\text{[math]}$ ，请计算本次测量结果的误差，并提出一条减小误差的合理化建议.
答案解析收藏纠错 + 选题

15. (2021·宛城模拟) 九年级数学兴趣小组的实践课题是“测量物体高度”.小组成员小明与小红分别采用不同的方案测量同一个底座为正方体的旗杆的高度，以下是他们研究报告的部分记录内容：

课题：测量旗杆的高度
	小明的研究报告	小红的研究报告
测量示意图
测量方案与测量数据	在点D处用距离地面高度为 $\text{[math]}$ 的测角仪测出旗杆顶端A的仰角 $\text{[math]}$ ，再用皮尺测得测角仪底部所在位置与旗杆底座正方体边缘的最短距离为 $\text{[math]}$ .	在点D处用距离地面高度为 $\text{[math]}$ 的测角仪测出旗杆顶端A的仰角 $\text{[math]}$ ，然后沿 $\text{[math]}$ 方向走 $\text{[math]}$ 到达点F处，测出旗杆顶端A的仰角 $\text{[math]}$ .
参考数据	$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，	$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
计算旗杆高度	$\text{[math]}$