小明遇到这样一个问题:
如图9-①,在△ABC中,AD平分∠BAC,∠ABC=2∠C,求证:AC=AB+BD;
小明通过思考发现,可以通过“截长、补短”两种方法解决问题:
方法一:如图9-②,在AC上截取AE,使得AE=AB,连接DE,可以得到全等三角形,进而解决问题;
方法二:如图9-③,延长AB到点E,使得BE=BD,连接DE,可以得到等腰三角形,进而解决问题.
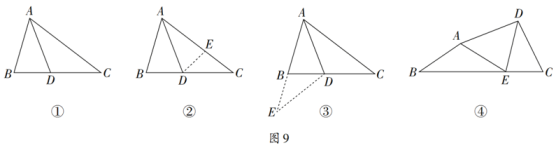
∠C=2∠B,∠DAE+∠B=90°,探究DC,CE,BE之间的数量关系,并证明.
例如: .
即: .
根据以上材料,解答下列问题:
在因式分解中,把多项式中的某些部分看作是一个整体,用一个新的字母代替(即“换元”),这样不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.下面是小林同学用“换元法”对多项式 解:设 原式 |
任务:(1)小林同学因式分解的结果彻底吗?若不彻底,请你写出该因式分解的最后结果:____.
【材料】教材中这样写道:“我们把多项式
及
叫做完全平方式”,如果关于某一字母的二次多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.例如:分解因式
.
原式 .
【材料】因式分解:
解:把看成一个整体,令
, 则
原式 , 再将
重新代入,得:原式
上述解题用到的“整体思想”是数学解题中常见的思想方法.请你解答下列问题:

如: ,
;
解决下列问题:
如: ,
;
解决下列问题:
已知=
, 求
的值.
解:由=
, 知x≠0,∴
, 即x+
=3.
∴=32﹣2=7,∴
=
.
以上解法中,是先将已知等式的两边“取倒数”,然后求出所求式子倒数的值,我们把此题的这种解法叫做“倒数法”,请你利用“倒数法”解决下面问题: