
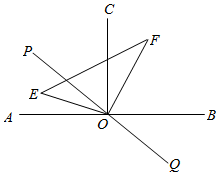

①若 平分
, 求α;
②若 , 求α.
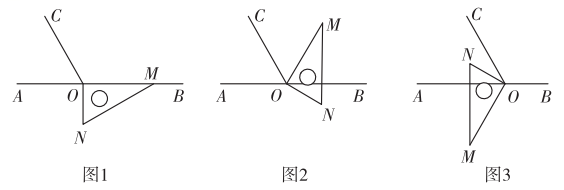
①若经过t秒后线段ON在∠AOC的内部,且∠AOM=3∠NOC,求t的值;
②在三角板转动时,射线OC同时绕点O以每秒4°的速度按顺时针方向旋转,当三角板停止转动时,射线OC也停止转动.经过t秒直线ON恰好平分∠AOC,请直接写出满足条件的t的值.

【知识运用】

①是否存在某个时刻t(秒),使得∠COD的度数是 , 若存在,求出
的值,若不存在,请说明理由;
②当为多少秒时,射线OC、OD、OA中恰好有一条射线是另一条射线的友好线.
①用含的代数式表示射线
和射线
重合前
和
的度数;
②整个旋转过程中,当满足时,求出相应的
的值.
①当为何值时,点
是线段
的三等分点.
②在点 , 点
开始出发的同时,点
也从点
出发,以每秒
的速度沿射线
方向运动,在运动过程中,点
, 点
分别是
,
的三等分点,请直接写出
的值.

如图1,若射线、
在
的内部,且
, 则
是
的内半角.
根据以上信息,解决下面的问题:
