… | 0.0001 | 0.01 | 1 | 100 | 10000 | … | |
… | 0.01 | x | 1 | y | 100 | … |
表格中x=,y=.
被开方数的小数点每向右移动2位,相应的算术平方根的小数点就向移动位.
①已知 , 则
;
②已知 ,
, 则m=.
例:将化为分数形式.
设 , 由
可知,
, 所以
, 解得
于是,得
根据以上阅读,回答下列问题:以下计算结果都用最简分数表示
… | 0.0001 | 0.01 | 1 | 100 | 10000 | … | |
… | 0.01 | x | 1 | y | 100 | … |
表格中 ,
.
(2)归纳总结:
被开方数的小数点每向右移动2位,相应的算术平方根的小数点就向 移动 位.
(3)规律运用:
①已知 , 则
;
②已知 ,
, 则
.
![]()
一天,豆豆去问奶奶的年龄,奶奶说:“我若是你现在这么大,你还要35年才出生;你若是我现在这么大,我就109岁啦!”请问豆豆现在多少岁了?(画出数轴会更方便)
如图,点C,D 均在线段AB 上且点C 在点 D 左侧,若AC=BD,CD=6 cm,AB=9 cm,则线段AC 的长为 cm。
已知点C,D 均在线段AB 上且点C 在点D 左侧,若AC=BD,CD=a( cm),AB=b( cm)(b>a),则线段AC 的长为 cm(用含a,b 的代数式表示)。
已知七年级某班共有m人,在本班参加拓展课报名统计时发现,选择围棋课的人数是n(n<m),其中未参加围棋课的男生人数是参加围棋课男生人数的一半,参加围棋课的女生人数是女生总人数的 , 求m与n 的数量关系。小聪同学在思考这个问题时联想到了上面的几何问题,并将这个实际问题转化为几何模型来解决,请你建立这个几何模型并求解。
问题情境:“综合与实践”课上,老师请同学们观察两个问题.
问题1:已知 ,
平分
,
平分
, 则
_______.
问题2:已知 , 点C是
的中点,点D是
的中点,则
_______.
数学思考:(1)完成问题1与问题2的填空.
深入探究:同学们通过观察,发现了这两个问题的联系.
(2)老师请同学们继续思考下面的问题,并提出一个与它有联系的问题.
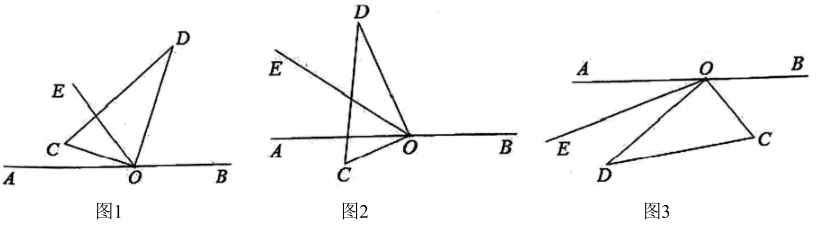
如图1,点O在直线上,
(
在直线
同侧),
分别平分
. 求
的度数(无需作答).
完成下列问题的解答:
①“运河小组”提出问题:如图2,线段 , 点C,D在线段
上(
),
, 点E,F分别是线段
的中点,求
的长.
②“武林小组”提出问题:如图3,点O在直线上,
(
在直线
两侧),
分别平分
. 求
的度数.

【情境描述】
圆圆想把一些相同规格的塑料杯,尽可能多地放入高的柜子里(如图1).她把杯子如图这样整齐地叠放成一摞(如图2),但她不知道一摞最多能叠几个可以一次性放进柜子里.
【观察发现】
圆圆测量后发现,按这样叠放,这摞杯子的总高度随着杯子数量的变化而变化,记录的数据如下表所示:
杯子的数量x(只) | 1 | 2 | 3 | 4 | 5 | 6 | … |
总高度h(cm) | 10 | 11.4 | 12.8 | 14.2 | 15.6 | 17 | … |
【数学思考】
(1)观察这些表格中数据的规律,用含x的代数式表示h;
(2)当杯子的数量为12只时,求这摞杯子的总高度.
【解决问题】
(3)请帮圆圆算一算,一摞最多能叠几个杯子,可以一次性放进柜子里?

如何设计奖品购买及兑换方案? | ||
素材 1 | 文具店销售某种钢笔与笔记本,已知钢笔每支 10 元,笔记本每本 5 元. | |
素材 2 | 学校用 1100 元购买这种钢笔和笔记本, 其数量之比为 | |
素材 3 | 文具店开展 "满送" 优惠活动,每满 130 元送1 张兑换券, 满 260 元送 2 张兑换券, 以此类推. 学校花费 1100 元后, 将兑换券全部用于商品兑换最终, 笔记本与钢笔数量相同. |
|
问题情境:“综合与实践”课上,老师提出如下问题:将一直角三角板的直角顶点放在直线
上,
,
是三角板的两条直角边,三角板可绕点
任意旋转,射线
平分
. 当三角板绕点
旋转到图1的位置时,
, 试求
的度数;
【背景素材】某公司要生产某大型产品60件,已知甲,乙,丙三家子工厂完成一件产品的时间分别为4天,6天,5天.现计划:①三家子工厂同时开始生产;②分配给甲工厂的数量是丙的2倍.
【问题解决】为设计方案,可以通过特殊情况或满足部分条件逐步进行探究.
时钟里的数学问题 | ||
素材1 | 时钟是我们口常生活中常用的生活用品。钟表上的时针和分针都绕其轴心旋转,如图.表盘中1-12匀分布,分针60分钟转动一周是360°,时针60分钟移动一周的 |
|
素材2 | 当时钟显示10:10时(如图).时针与分针所成角度多少度?解决这个问题,可以先考虑10:00时,时针与分针所成角度为60°;从10:00到10:10.分针转动的角度为 |
|
素材3 | 当时针和分针所成角度180°时,我们将这样的时刻称为“美妙时刻”。如图.当时钟显示6:00时,此时,时针和分针所成角度180°,因此6:00就是一个美妙时刻. |
|
解决问题 | ||
任务1 | 当时钟显示1:10分时,求时针与分针所成角度. | |
任务2 | 时钟显示1:00时,时针与分针所成角度为30°,在1:00到1:30的30分钟内,小明发现存在着时针和分针册直的情况,请求出此时的时刻。 | |
任务3 | 6:00之后的下一个美妙时刻是 ▲ , 一天24个小时内,共有 ▲ 个美妙时刻。 | |
则A , B两点之间的距离为,线段的中点表示的数为;
当 , 则A , B两点之间的距离为
;
当 , 则A , B两点之间的距离为
;
当 , 则A , B两点之间的距离为
;
②【类比探究】:线段的中点表示的数为(用含a , b的代数式表示);
点M从点A出发,以每秒1个单位长度的速度向左匀速运动,
同时,点N从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,
当M , N两点相遇时,均停止运动,设运动时间为t秒(),点M , N在运动过程中;
①M , N两点之间的距离为;(用含t的代数式表示)
②若点C为的中点,点D为
的中点,线段
的长度为(用含t的代数式表示).

如图1,若射线、
在
的内部,且
, 则
是
的内半角.
根据以上信息,解决下面的问题:
问题 背景 | 吴兴区某学校决定在校内开辟劳动实践基地,现向全校师生征集实践基地的设计方案.学校项目化学习小组根据学校要求完成了初步设计,请跟随小组成员共同完成以下任务. |
素材一 | 项目化学习小组通过初步研讨,计划利用学校现成的一堵“L”型墙面和栅栏围成长方形的劳动实践基地
|
素材二 | 通过查询学校现有物资信息,学校仓库可提供栅栏的总长度为10米.项目化学习小组决定将这10米栅栏全部用于劳动实践基地中. |
素材三 | 经过市场调查,建造劳动实践基地的人工和材料费合计为25元/平方米. |
任务一 | 根据图1的设计, 若设 在②中,长方形 |
任务二 | 根据学校要求,劳动实践基地的长 |
任务三 | 在任务二的条件下,为了节省学校的开支,请你帮助小组成员确定符合要求的方案: (填①或②),并求出此时所需的费用. |