4.
(2024高三下·成都模拟)
2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日

点的轨道运行.

点是平衡点,位于地月连线的延长线上.设地球质量为M
1 , 月球质量为M
2 , 地月距离为R,

点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
 .设
.设  ,由于
,由于  的值很小,因此在近似计算中
的值很小,因此在近似计算中  ,则r的近似值为( )
,则r的近似值为( )
.设
,由于
的值很小,因此在近似计算中
,则r的近似值为( )

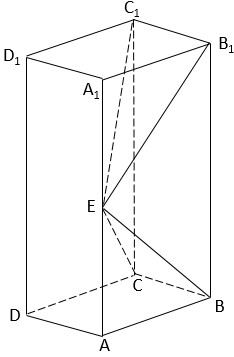
是直角三角形;
面积的最大值.