| 队员1 | 队员2 | 队员3 | 队员4 | 队员5 | 队员6 | |
| 甲队 | 176 | 175 | 174 | 172 | 175 | 178 |
| 乙队 | 170 | 176 | 173 | 174 | 180 | 177 |
设这两队队员平均数依次为 ,
,身高的方差依次为
,
,则下列关系中,完全正确的是( )
 B .
B .  C .
C .  D .
D . 

①直接写出 的边BC上的高h的值;
②当点E从点D向点A运动的过程中,下面关于四边形AFCE的形状的变化的说法中,正确的是
A.平行四边形→矩形→平行四边形→菱形→平行四边形
B.平行四边形→矩形→平行四边形→正方形→平行四边形
C.平行四边形→菱形→平行四边形→菱形→平行四边形
D.平行四边形→菱形→平行四边形→矩形→平行四边形
①求点Q的坐标(用含t的式子表示)
②直接写出线段PQ的长(用含t的式子表示)
如图,一片树叶的长是指沿叶脉方向量出的最长部分的长度(不含叶柄),树叶的宽是指沿与主叶脉垂直方向量出的最宽处的长度,树叶的长宽比是指树叶的长与树叶的宽的比值。

某同学在校园内随机收集了A树、B树、C树三棵的树叶各10片,通过测量得到这些树叶的长y(单位:cm),宽x(单位:cm)的数据,计算长宽比,理如下:
表1 A树、B树、C树树叶的长宽比统计表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| A树树叶的长宽比 | 4.0 | 4.9 | 5.2 | 4.1 | 5.7 | 8.5 | 7.9 | 6.3 | 7.7 | 7.9 |
| B树树叶的长宽比 | 2.5 | 2.4 | 2.2 | 2.3 | 2.0 | 1.9 | 2.3 | 2.0 | 1.9 | 2.0 |
| C树树叶的长宽比 | 1.1 | 1.2 | 1.2 | 0.9 | 1.0 | 1.0 | 1.1 | 0.9 | 1.0 | 1.3 |
表1 A树、B树、C树树叶的长宽比的平均数、中位数、众数、方差统计表
| 平均数 | 中位数 | 众数 | 方差 | |
| A树树叶的长宽比 | 6.2 | 6.0 | 7.9 | 2.5 |
| B树树叶的长宽比 | 2.2 | 0.38 | ||
| C树树叶的长宽比 | 1.1 | 1.1 | 1.0 | 0.02 |
A树、B树、C树树叶的长随变化的情况
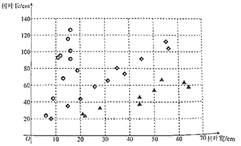
解决下列问题:
②小李同学说:“从树叶的长宽比的平均数来看,我认为,下图的树叶是B树的树叶。”
![]()
请你判断上面两位同学的说法中,谁的说法是合理的,谁的说法是不合理的,并给出你的理由;
求证:① ;
② ;
|
候选人 |
甲 |
乙 |
|
|
测试成绩(百分制) |
面试成绩 |
86 |
92 |
|
笔试成绩 |
90 |
83 |
|
某公司认为,招聘公关人员,面试成绩应该比笔试成绩重要,如果面试和笔试的权重分别是6和4,根据两人的平均成绩,这个公司将录取。

小明根据学习函数的经验,分别对这两种函数随自变量的变化而变化的情况进行了探究,下面是小明探究过程,请补充完整:
①按下表自变量的值进行取点、画图、测量,得到了 与x的几组对应值:
| x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| | 1.12 | 0.5 | 0.71 | 1.12 | 1.58 | 2.06 | 2.55 | 3.04 |
②在所给坐标系中描出补全后的表中的各对应值为坐标的点,画出函数 的图象;

在同一坐标系中,画出函数 的图象;
①函数 的最小值是;
②函数 的图象与函数
的图象的交点表示的含义是;
③若 ,AP的长约为cm

①下列四个点 ,
,
,
中,与点A是“中心轴对称”的是;
②点E在射线OB上,若点E与正方形ABCD是“中心轴对称”的,求点E的横坐标 的取值范围;