江苏省兴化市乐吾实验学校、芙蓉外国语实验学校2020-202...

更新时间：2024-07-31 浏览次数：249 类型：月考试卷

一、选择题

1. (2024七下·顺德月考) 下列倡导节约的图案中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020八上·兴化月考) 下列命题中，是假命题的是（）

A . 在△ABC中，若∠A：∠B：∠C＝1：2：3，则△ABC是直角三角形 B . 在△ABC中，若a²＝(b＋c) (b－c)，则△ABC是直角三角形 C . 在△ABC中，若∠B＝∠C＝∠A，则△ABC是直角三角形 D . 在△ABC中，若a：b：c＝5：4：3，则△ABC是直角三角形

答案解析收藏纠错 + 选题
3. (2020八上·兴化月考) 如图，DE是△ABC的边AB的垂直平分线，点D为垂足，DE交AC于点E，且AC＝8，BC＝5，则△BEC的周长是（）

A . 12 B . 13 C . 14 D . 15

答案解析收藏纠错 + 选题
4. (2020八上·佳木斯期末) 如图，OP平分∠AOB，PC⊥OA于点C，点D在OB上，PC＝3，则PD的取值范围是（）

A . PD≥3 B . PD＞3 C . PD≤3 D . 不能确定

答案解析收藏纠错 + 选题
5. (2021九上·榆树期末) 如图，在Rt△ABC中，CE是斜边AB上的中线，CD⊥AB ，若CD＝5，CE＝6，则△ABC的面积是（）

A . 24 B . 25 C . 30 D . 36

答案解析收藏纠错 + 选题
6. (2020八上·抚顺月考) 若一个等腰三角形的两边长分别为2，4，则第三边的长为（）

A . 2 B . 3 C . 4 D . 2或4

答案解析收藏纠错 + 选题
7. (2023八下·梁平期中)
如图，长为8cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3cm至D点，则橡皮筋被拉长了（　　）

A . 2cm B . 3cm C . 4cm D . 5cm

答案解析收藏纠错 + 选题
8. (2023八上·鲤城月考) 如图，∠AOB=60°，OA=OB，动点C从点O出发，沿射线OB方向移动，以AC为边在右侧作等边△ACD，连接BD，则BD所在直线与OA所在直线的位置关系是（）

A . 平行 B . 相交 C . 垂直 D . 平行、相交或垂直

答案解析收藏纠错 + 选题

二、填空题

9. (2020八上·兴化月考) 如图，△ABC与△A′B′C′关于直线l对称，且∠A＝102°，∠C′＝25°，则∠B的度数为

答案解析收藏纠错 + 选题
10. (2020八上·兴化月考) 如图，以直角三角形各边向外作正方形，其中两个正方形的面积分别为225和144，则正方形A的面积为.

答案解析收藏纠错 + 选题
11. (2020八上·兴化月考) 将一矩形纸条，按如图所示折叠，则∠1=度.

答案解析收藏纠错 + 选题
12. (2020八上·兴化月考) 如图Rt△ABC中，∠C＝90°，∠A＝30°，BD是∠ABC的平分线，若BD＝10，则AC＝.

答案解析收藏纠错 + 选题
13. (2020八上·兴化月考) 如图，OP平分∠AOB，PA $\text{[math]}$ OA，PB $\text{[math]}$ OB，垂足分别为点A、B.下列结论中，一定成立的是（填序号）
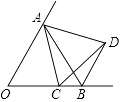
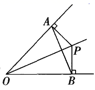
①PA＝PB；②OA＝OB；③OP垂直平分AB；④AB垂直平分OP

答案解析收藏纠错 + 选题
14. (2020八上·兴化月考) 如图，在△ABC中，AB＝6cm，AC＝4cm，BD平分∠ABC，CD平分∠ACB，EF过点D且EF∥BC，则△AEF的周长是cm.

答案解析收藏纠错 + 选题
15. (2020八上·兴化月考) “三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D、E可在槽中滑动。若∠BDE=75°，则∠CDE的度数是

答案解析收藏纠错 + 选题
16. (2021八上·姜堰月考) 如图，在正方形网格中有两个小正方形被涂黑，再涂黑一个图中其余的小正方形，使得整个被涂黑的图案构成一个轴对称图形，那么涂法共有种.

答案解析收藏纠错 + 选题
17. (2020八上·兴化月考) 如图Rt△ABC中，AC=12，BC=5，分别以AB，AC，BC为直径作半圆，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题
18. (2020八上·滦州期末) 如图，△ABC中，∠ACB＝90°，AB＝5cm，BC＝3cm，若点P从点A出发，以每秒2cm的速度由A向B运动，设运动时间为t秒（t＞0）.在运动过程中，当t为时，△BCP为等腰三角形.

答案解析收藏纠错 + 选题

三、解答题

19. (2020八上·兴化月考) 如图
1. （1）如图1，在△ABC中，利用直尺和圆规按要求作图（不写作法，保留作图痕迹）：
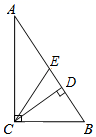
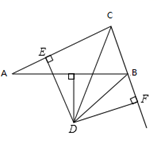
  ①在BC边上作点P，使得点P到AB和AC的距离相等；
  
  ②在射线AP上作点Q，使得AQ＝CQ.
2. （2）如图2，在△ABC中，∠A＝27°，∠C＝72°，请你在图2中画一条线段将△ABC分成两个等腰三角形，并标出等腰三角形顶角的度数.
答案解析收藏纠错 + 选题
20. (2020八上·兴化月考) 如图，在 $\text{[math]}$ 中，点D，E分别在边AC，AB上，BD与CE交于点O，给出下列三个条件：①∠EBO=∠DCO；② $\text{[math]}$ ；③ $\text{[math]}$ .
1. （1）上述三个条件中，由哪两个条件可以判定 $\text{[math]}$ 是等腰三角形？（用序号写出所有成立的情形）
2. （2）请选择（1）中的一种情形，说明你的理由.
答案解析收藏纠错 + 选题
21. (2021八上·镇原期中) 如图，△ABC中，∠ACB=90°，AD平分∠BAC，DE⊥AB于E，
1. （1）若∠BAC=50°，求∠EDA的度数；
2. （2）求证：直线AD是线段CE的垂直平分线．
答案解析收藏纠错 + 选题
22. (2020八上·兴化月考) 八年级（2）班的小明和小亮同学学了“勾股定理”之后，为了测得图中风筝的高度 $\text{[math]}$ ，他们进行了如下操作：①测得 $\text{[math]}$ 的长为 $\text{[math]}$ 米（注： $\text{[math]}$ ）；②根据手中剩余线的长度计算出风筝线 $\text{[math]}$ 的长为 $\text{[math]}$ 米；③牵线放风筝的小明身高 $\text{[math]}$ 米.
1. （1）求风筝的高度 $\text{[math]}$ .
2. （2）过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，求 $\text{[math]}$ 、 $\text{[math]}$ .
答案解析收藏纠错 + 选题
23. (2023八下·北京市期中) 如图，在△ABC中，AB＝4，AC＝3，BC＝5，DE是BC的垂直平分线，DE分别交BC、AB于点D、E.
1. （1）求证：△ABC为直角三角形．
2. （2）求AE的长．
答案解析收藏纠错 + 选题
24. (2020八上·兴化月考) 如图，△ABC是等腰直角三角形，AB=AC，D是斜边BC的中点，E、F分别是AB、AC边上的点，且AE+AF=AB，
1. （1）求证：DE⊥DF；
2. （2）若AC=2，求四边形DEAF的面积.
答案解析收藏纠错 + 选题
25. (2020八上·兴化月考) 已知：如图，△ABC中∠ACB的平分线与AB的垂直平分线交于点D，DE⊥AC于点E，DF⊥BC交CB的延长线于点F.
1. （1）求证：AE＝BF；
2. （2）若AC＝24，BC＝10，求AE的长.
答案解析收藏纠错 + 选题
26. (2020八上·兴化月考) 如图，在△ABC中，AB＝AC，∠BAC＝80°，点D为△ABC内一点，∠ABD＝∠ACD＝20°，E为BD延长线上的一点，且AB＝AE.
1. （1）求∠BAD的度数；
2. （2）求证：DE平分∠ADC；
3. （3）请判断AD，BD，DE之间的数量关系，并说明理由.
答案解析收藏纠错 + 选题
27. (2020八上·兴化月考) 在四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1） P为边BC上一点，将 $\text{[math]}$ 沿直线AP翻折至 $\text{[math]}$ 的位置 $\text{[math]}$ 点B落在点E处 $\text{[math]}$
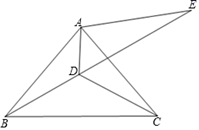
  $\text{[math]}$ 如图1，当点E落在CD边上时，利用尺规作图，在图1中作出满足条件的图形 $\text{[math]}$ 不写作法，保留作图痕迹，用2B铅笔加粗加黑 $\text{[math]}$ 并直接写出此时 $\text{[math]}$ _▲_；
  
  $\text{[math]}$ 如图2，若点P为BC边的中点，连接CE，则CE与AP有何位置关系？请说明理由；
2. （2）点Q为射线DC上的一个动点，将 $\text{[math]}$ 沿AQ翻折，点D恰好落在直线BQ上的点 $\text{[math]}$ 处，则 $\text{[math]}$ ；
答案解析收藏纠错 + 选题