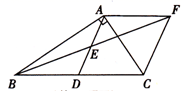
①四边形 有可能成为正方形;②
是等腰直角三角形;③四边形
的面积是定值;④点
到线段
的最大距离为
.
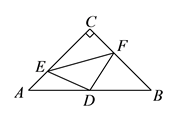



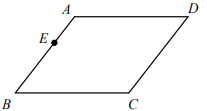
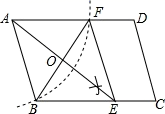
已知:平行四边形 .
求作:点 ,使点
为边
的中点.
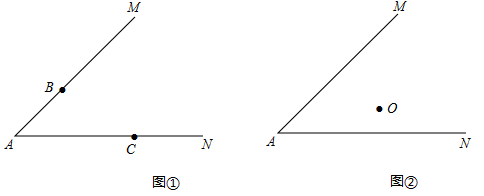
作法:如图,
①作射线 ;
②以点 为圆心,
长为半径画弧,
交 的延长线于点
;
③连接 交
于点
.
所以点 就是所求作的点.
根据小东设计的尺规作图过程,

证明:连接 ,
.
四边形
是平行四边形,
.
▲ ,
四边形
是平行四边形
▲
(填推理的依据).
▲
(填推理的依据).
点
为所求作的边
的中点.
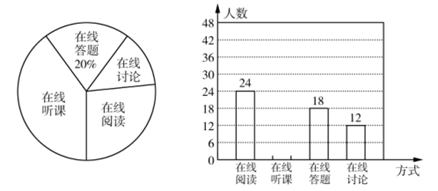
根据图中信息,解答下列问题:
①y与x的函数表达式为;②自变量x的取值范围是.
x | … | | | | 1 | 2 | 3 | 4 | … |
y | … | | | 5 | 4 | m | | | … |
①写出m的值;
②画出函数图象;
③观察图象,写出该函数两条不同类型的性质.
如图,在平面直角坐标系中,正比例函数y=kx(k>0)与反比例函数y= 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m , 0).其中m>0.

【动手操作】小明同学在探究证明中位线性质定理时,是沿着中位线将三角形剪开然后将它们无缝隙、无重叠的拼在一起构成平行四边形,从而得出:三角形中位线平行于第三边且等于第三边的一半.
【性质证明】小明为证明定理,他想利用三角形全等、平行四边形的性质来证明.请你帮他完成解题过程(要求:画出图形,根据图形写出已知、求证和证明过程).