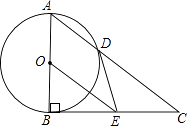
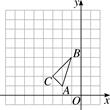
在平面直角坐标系xOy中,⊙C的半径为r,点P是与圆心C不重合的点,给出如下定义:若点P′为射线CP上一点,满足CP•CP′=r2 , 则称点P′为点P关于⊙C的反演点.右图为点P及其关于⊙C的反演点P′的示意图.

(1)如图2,当⊙O的半径为1时,分别求出点M(1,0),N(0,2),T( ,
)关于⊙O的反演点M′,N′,T′的坐标;
(2)如图3,已知点A(1,4),B(3,0),以AB为直径的⊙G与y轴交于点C,D(点C位于点D下方),E为CD的中点.
①若点O,E关于⊙G的反演点分别为O′,E′,求∠E′O′G的大小;
②若点P在⊙G上,且∠BAP=∠OBC,设直线AP与x轴的交点为Q,点Q关于⊙G的反演点为Q′,请直接写出线段GQ′的长度.
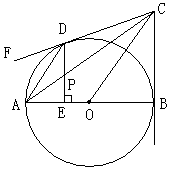
如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(4,0)两点,与y轴交于点C,且OC=3OA,点P是抛物线上的一个动点,过点P作PE⊥x轴于点E,交直线BC于点D,连接PC.
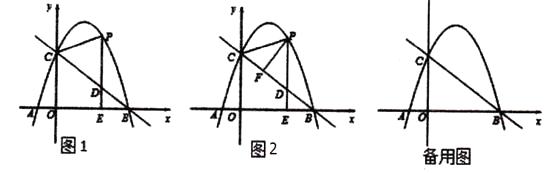
已知:如图①,在平行四边形ABCD中,AB=12,BC=6,AD⊥BD.以AD为斜边在平行四边形ABCD的内部作Rt△AED,∠EAD=30°,∠AED=90°.
(1)求△AED的周长;
(2)若△AED以每秒2个单位长度的速度沿DC向右平行移动,得到△A0E0D0 , 当A0D0与BC重合时停止移动,设运动时间为t秒,△A0E0D0与△BDC重叠的面积为S,请直接写出S与t之间的函数关系式,并写出t的取值范围;
(3)如图②,在(2)中,当△AED停止移动后得到△BEC,将△BEC绕点C按顺时针方向旋转α(0°<α<180°),在旋转过程中,B的对应点为B1 , E的对应点为E1 , 设直线B1E1与直线BE交于点P、与直线CB交于点Q.是否存在这样的α,使△BPQ为等腰三角形?若存在,求出α的度数;若不存在,请说明理由.
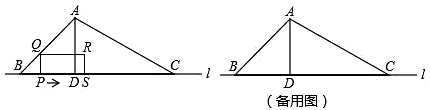
已知y是x的函数,下表是y与x的几组对应值.
|
x |
… |
﹣5 |
﹣4 |
﹣3 |
﹣2 |
0 |
1 |
2 |
3 |
4 |
5 |
… |
|
y |
… |
1.969 |
1.938 |
1.875 |
1.75 |
1 |
0 |
﹣2 |
﹣1.5 |
0 |
2.5 |
… |
小孙同学根据学习函数的经验,利用上述表格反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.

下面是小孙同学的探究过程,请补充完整;
①x=﹣1时,对应的函数值y的为;
②若函数值y>0,则x的取值范围是;
③写出该函数的一条性质(不能与前面已有的重复):.

问题1:请用9个边长为1的小正方形在图(2)的位置拼成一个大正方形.

计算:拼成的大正方形的面积为5,边长为 ,可表示成
;
剪切:如图(3)将5个小正方形按如图所示分成5部分,虚线为剪切线;
拼图:以图(3)中的虚线为边,拼成一个边长为 的大正方形,如图(4).

问题2:请仿照上面的研究方式,用13个边长为1的小正方形剪拼成一个大正方形;
①计算:拼成的大正方形的面积为,边长为,可表示成;
②剪切:请仿照图(3)的方法,在图(5)的位置画出图形.
③拼图:请仿照图(4)的方法,在图(6)的位置出拼成的图.
|
锐角 | | | |
| | |||
| | |||
| |