2021年秋季浙教版数学九年级上学期期中测试模拟卷（适合绍兴...

更新时间：2021-10-25 浏览次数：145 类型：期中考试

一、单选题

1. (2020九上·河西期末) 当 $\text{[math]}$ 时，二次函数 $\text{[math]}$ 有（）

A . 最大值-3 B . 最小值-3 C . 最大值-4 D . 最小值-4

答案解析收藏纠错 + 选题
2. (2021·富拉尔基模拟) 一个不透明的盒子里有若干个黑球和3个白球，3个红球，它们除颜色外没有其他区别，若从这个盒子里随机摸出一个黑球的概率是 $\text{[math]}$ ，则这个盒子里黑球的个数为（）

A . 12个 B . 9个 C . 6个 D . 3个

答案解析收藏纠错 + 选题
3. (2020·莆田模拟) 已知点 $\text{[math]}$ ， $\text{[math]}$ 在二次函数 $\text{[math]}$ 的图象上，点 $\text{[math]}$ 是函数图象的顶点，则（）

A . 当 $\text{[math]}$ 时， $\text{[math]}$ 的取值范围是 $\text{[math]}$ B . 当 $\text{[math]}$ 时， $\text{[math]}$ 的取值范围是 $\text{[math]}$ C . 当 $\text{[math]}$ 时， $\text{[math]}$ 的取值范围是 $\text{[math]}$ D . 当 $\text{[math]}$ 时， $\text{[math]}$ 的取值范围是 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021九上·通榆月考) 将抛物线y=x²向右平移1个单位长度后，所得到的抛物线的解析式是（）

A . y=x²-1 B . y=x²-1 C . y=(x-1)² D . y=(x+1)²

答案解析收藏纠错 + 选题
5. (2024九下·莒南模拟) 二次函数 $\text{[math]}$ （ $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 是常数，且 $\text{[math]}$ ）的自变量 $\text{[math]}$ 与函数值 $\text{[math]}$ 的部分对应值如下表：

$\text{[math]}$

…

$\text{[math]}$

0

1

2

…

$\text{[math]}$

…

$\text{[math]}$

2

2

$\text{[math]}$

…

且当 $\text{[math]}$ 时，对应的函数值 $\text{[math]}$ .有以下结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③关于 $\text{[math]}$ 的方程 $\text{[math]}$ 的负实数根在 $\text{[math]}$ 和0之间；④ $\text{[math]}$ 和 $\text{[math]}$ 在该二次函数的图象上，则当实数 $\text{[math]}$ 时， $\text{[math]}$ .其中正确的结论是（）

A . ①② B . ②③ C . ③④ D . ②③④

答案解析收藏纠错 + 选题
6. (2021九上·余姚期中) $\text{[math]}$ ，过 $\text{[math]}$ 、 $\text{[math]}$ 两点画半径为 $\text{[math]}$ 的圆，能画的圆的个数为（）

A . 0个 B . 1个 C . 2个 D . 无数个

答案解析收藏纠错 + 选题
7. (2021九上·印台期末) 如图所示，中堂中学教学楼前喷水池喷出的抛物线形水柱，水柱喷出的竖直高度y（m）与水平距离x（m）满足y＝﹣（x﹣2）²+6，则水柱的最大高度是（　　）

A . 2 B . 4 C . 6 D . 2+ $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021·深圳模拟) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是等圆， $\text{[math]}$ 内接于 $\text{[math]}$ ，点C ， E分别在 $\text{[math]}$ ， $\text{[math]}$ 上．如图，①以C为圆心， $\text{[math]}$ 长为半径作弧交 $\text{[math]}$ 于点D ，连接 $\text{[math]}$ ；②以E为圆心， $\text{[math]}$ 长为半径作弧交 $\text{[math]}$ 于点F ，连接 $\text{[math]}$ ；下面有四个结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ，所有正确结论的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
9. (2020九上·怀集期中) 如图，一次函数 $\text{[math]}$ 与二次函数为 $\text{[math]}$ 的图象相交于点M，N，则关于x的一元二次方程 $\text{[math]}$ 的根的情况是（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 没有实数根 D . 有两个实数根

答案解析收藏纠错 + 选题
10. (2021·滦州模拟) 如图，是反比例函数 $\text{[math]}$ 图象，阴影部分表示它与横纵坐标轴正半轴围成的区域，在该区域内 $\text{[math]}$ 不包括边界 $\text{[math]}$ 的整数点个数是k，则抛物线 $\text{[math]}$ 向上平移k个单位后形成的图象是 $\text{[math]}$ 　　 $\text{[math]}$

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

11. (2023九上·秦都期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ =.

答案解析收藏纠错 + 选题

12. (2021·北京模拟) 在就地过年倡议下，更多游客缩小出游半径，本地游、近郊游、周边游取代异地长线游，成为牛年出行新趋势．某地区对近郊游的住宿环境、餐饮、服务等方面对所住游客进行了综合满意度调查，在甲，乙两个景点都去过的的游客中随机抽取了100人，每人分别对这两个景点进行了评分，统计如下：

	非常满意	较满意	一般	不太满意	非常不满意	合计
甲	28	40	10	10	12	100
乙	25	20	45	6	4	100

若小聪要在甲，乙两个景点中选择一个景点，根据表格中数据，你建议她去景点（填甲或乙），理由是．

答案解析收藏纠错 + 选题

13. (2021·上城模拟) 在⊙O中，AB是直径，AB＝2，C是圆上除A、B外的一点，D、E分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点，M是弦DE的中点，则CM的取值范围是.

答案解析收藏纠错 + 选题
14. (2020八上·三水期中) 如图Rt△ABC ， ∠C＝90°，分别以各边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”：当AC＝3，BC＝4时，则阴影部分的面积为．

答案解析收藏纠错 + 选题
15. (2020九上·南京期中) 如图所示，在⊙O中，AB为弦，OC⊥AB交AB于点D，且OD=DC，P为⊙O上任意一点，连接PA，PB，若⊙O的半径为1，则S_△_PAB的最大值为.

答案解析收藏纠错 + 选题
16. (2023九上·兰溪月考) 定义：在平面直角坐标系中，我们将横、纵坐标都是整数的点称为“整点”.若抛物线y＝ax²﹣2ax+a+3与x轴围成的区域内(不包括抛物线和x轴上的点)恰好有8个“整点”，则a的取值范围是.

答案解析收藏纠错 + 选题

三、解答题

17. (2019九上·秀洲期末) 已知二次函数y=x²+3x+m的图象与x轴交于点A（﹣4，0）．
1. （1）求m的值；
2. （2）求该函数图象与坐标轴其余交点的坐标．
答案解析收藏纠错 + 选题
18. (2021·泰州模拟) 袋中有1个红球和2个黑球，这些球除颜色外都相同.小明做摸球实验：他搅匀后从中任意摸出1个球，记录颜色后放回、搅匀，再从中任意摸出1球.像这样连续摸两次算一次实验.若摸出红球得2分，摸出黑球得1分.
1. （1）求两次摸球所得总分是4分的概率；
2. （2）若要使每次摸球实验所得总分不少于3分，如何改变袋中球的情况？
答案解析收藏纠错 + 选题
19. (2020九上·绥滨期末) 已知二次函数 $\text{[math]}$ 的图象如图所示，它与x轴的一个交点的坐标为（－1，0），与y轴的交点坐标为（0，－3）
1. （1）求此二次函数的解析式；
2. （2）求此二次函数的图象与x轴的另一个交点的坐标
3. （3）根据图象回答：当x取何值时，y＜0？
答案解析收藏纠错 + 选题
20. (2021八下·曲阳期末) 已知在Rt△ABC中，∠ACB=90°，现按如下步骤作图：
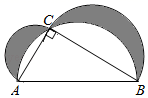
①分别以A，C为圆心，a为半径（a＞ $\text{[math]}$ AC）作弧，两弧分别交于M，N两点；
②过M，N两点作直线MN交AB于点D，交AC于点E；
③将△ADE绕点E顺时针旋转180°，设点D的像为点F．
1. （1）请在图中直线标出点F并连接CF；
2. （2）求证：四边形BCFD是平行四边形；
3. （3）当∠B为多少度时，四边形BCFD是菱形．
答案解析收藏纠错 + 选题
21. (2020九上·新余月考) 某河上有抛物线形拱桥，当水面离拱顶5m时，水面宽8m．一木船宽4m，高2m，载货后，木船露出水面的部分为 $\text{[math]}$ m．以拱顶O为坐标原点建立如图所示的平面直角坐标系，A、B为抛物线与水面的交点．
1. （1） B点的坐标为；
2. （2）求抛物线解析式；
3. （3）当水面离拱顶1.8米时，木船能否通过拱桥？
答案解析收藏纠错 + 选题
22. (2021九上·南宁期中) 某超市销售一种商品，每件成本为50元，销售人员经调查发现，销售单价为100元时，每月的销售量为50件，而销售单价每降低2元，则每月可多售出10件，且要求销售单价不得低于成本．
1. （1）求该商品每月的销售量y（件）与销售单价x（元）之间的函数关系式；（不需要求自变量取值范围）
2. （2）若使该商品每月的销售利润为4000元，并使顾客获得更多的实惠，销售单价应定为多少元？
3. （3）超市的销售人员发现：当该商品每月销售量超过某一数量时，会出现所获利润反而减小的情况，为了每月所获利润最大，该商品销售单价应定为多少元？
答案解析收藏纠错 + 选题
23. (2021·苏州模拟) 我们知道：有一内角为直角的三角形叫做直角三角形.类似地，我们定义：有一内角为45°的三角形叫做半直角三角形.如图，在平面直角坐标系中，O为原点，A(4，0)，B(﹣4，0)，D是y轴上的一个动点，∠ADC=90°(A、D、C按顺时针方向排列)，BC与经过A、B、D三点的⊙M交于点E，DE平分∠ADC，连结AE，BD.显然△DCE、△DEF、△DAE是半直角三角形.
1. （1）求证：△ABC是半直角三角形；
2. （2）求证：∠DEC=∠DEA；
3. （3）若点D的坐标为(0，8)，求AE的长.
答案解析收藏纠错 + 选题
24. (2022九下·龙凤期中) 如图，二次函数 $\text{[math]}$ 的图象与一次函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ 、 $\text{[math]}$ （点 $\text{[math]}$ 在右侧），与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 的横坐标恰好为 $\text{[math]}$ .动点 $\text{[math]}$ 、 $\text{[math]}$ 同时从原点 $\text{[math]}$ 出发，沿射线 $\text{[math]}$ 分别以每秒 $\text{[math]}$ 和 $\text{[math]}$ 个单位长度运动，经过 $\text{[math]}$ 秒后，以 $\text{[math]}$ 为对角线作矩形 $\text{[math]}$ ，且矩形四边与坐标轴平行.
1. （1）求 $\text{[math]}$ 的值及 $\text{[math]}$ 秒时点 $\text{[math]}$ 的坐标；
2. （2）当矩形 $\text{[math]}$ 与抛物线有公共点时，求时间 $\text{[math]}$ 的取值范围；
3. （3）在位于 $\text{[math]}$ 轴上方的抛物线图象上任取一点 $\text{[math]}$ ，作关于原点 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，当点 $\text{[math]}$ 恰在抛物线上时，求 $\text{[math]}$ 长度的最小值，并求此时点 $\text{[math]}$ 的坐标.
答案解析收藏纠错 + 选题