 B .
B .  C .
C .  D .
D . 
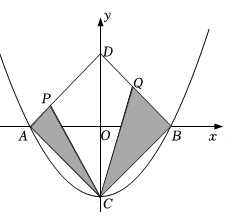

① ;②若
,则
;③对于任意
,始终有
;④若B的坐标为
,则C的坐标为
.
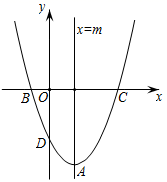

①图像与坐标轴的交点为(﹣1,0),(3,0)和(0,3);
②图像具有对称性,对称轴是直线x=1;
③当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大;
④当x=﹣1或x=3时,函数的最小值是0;
⑤当x=1时,函数的最大值是4;
⑥若点P(a,b)在该图像上,则当b=2时,可以找到4个不同的点P.其中错误的结论是 (填序号).

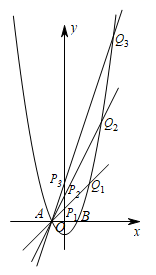

②抛物线y=x2+1与y=x2的“完美三角形”的斜边长的数量关系是 ▲ ;

①求a的值.
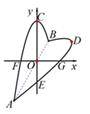
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段BF=2MF,求点M、N的坐标.
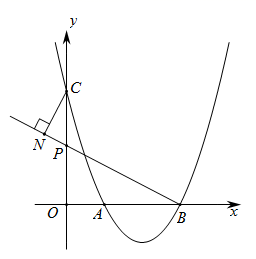
③如图3,点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,求点Q的坐标.