 B .
B .  C .
C . 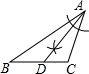 D .
D . 




 B .
B .  C .
C .  D .
D . 
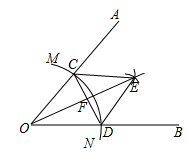
①CE∥OB;②CE=2CF;③∠AOE=∠BOE;④CD⊥OE.其中正确的有( )
 B .
B .  C .
C . 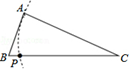 D .
D . 


![]()

⑴在CD边上找一点P,连结AP,使△AEP是等腰三角形;
⑵在AB边上找一点Q,使EQ⊥AP,画出线段EQ.
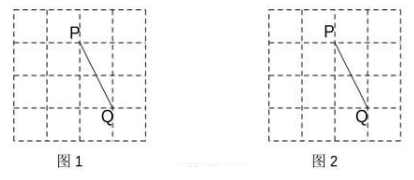



图1 图2
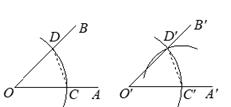
求作: ,使
,
,(用尺规作图,保留作图痕迹,不写作法).
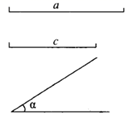
请你根据所学的知识,说明尺规作图作出 ,用到的是三角形全等判定定理中的_▲_,作出的
是唯一的,依据是三角形全等判定定理中的_▲_.

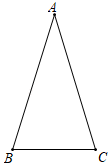
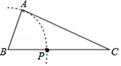
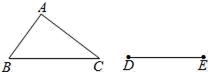
①作△ABC的角平分线AD;
②作边AB的垂直平分线EF , EF与AD相交于点P;
③连接PB , PC .
请你观察图形解答下列问题:
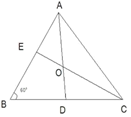

已知:如图,线段AB和直线且点B在直线上
求作:点C,使点C在直线上并且使△ABC为等腰三角形.
作图要求:保留作图痕迹,不写作法,做出所有符合条件的点C.
如图一,当∠1=90°时,符合(1)中条件的点C有个;如图二,当∠1=60°时,符合(1)中条件的点C有个.
如图,∠AOB=45°,点M,N在射线OA上,OM=x,ON=x+2,点P是射线OB上的点.若使点P,M,N构成等腰三角形的点P有且只有三个,求x的值.