2022-2023学年浙教版数学八上期末复习专题一次函数的...

更新时间：2022-11-19 浏览次数：121 类型：复习试卷

一、单选题（每题2分，共20分）

1. (2021八上·驻马店期末) 如图，一次函数y＝ax+b的图象与y＝cx+d的图象如图所示且交点的横坐标为4，则下列说法正确的个数是（　　）

①对于函数y＝ax+b来说，y随x的增大而减小；②函数y＝ax+d不经过第一象限；③方程ax+b=cx+d的解是x=4；④ d-b=4（a-c）.

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
2. (2021八上·文山期末) 如图，直线l是一次函数 $\text{[math]}$ 的图象，下列说法中，错误的是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . 若点（－1， $\text{[math]}$ ）和点（2， $\text{[math]}$ ）是直线l上的点，则 $\text{[math]}$ C . 若点（2，0）在直线l上，则关于x的方程 $\text{[math]}$ 的解为 $\text{[math]}$ D . 将直线l向下平移b个单位长度后，所得直线的解析式为 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023八上·义乌期末) 如图，函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ ，则不等式 $\text{[math]}$ 的解集为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021八上·东至期末) 如图，观察图象，可以得出不等式组 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 0＜x＜2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021八上·凤阳期末) 如果一次函数y＝3x＋6与y＝2x－4的图象交点坐标为（a，b），则 $\text{[math]}$ 是方程组（）的解

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021八上·宣城期末) 如图，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，则关于x，y的方程组 $\text{[math]}$ 的解为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021八下·临海期中) 一辆轿车和一辆货车分别从甲、乙两地同时出发，匀速相向而行，相遇后继续前行，已知两车相遇时轿车比货车多行驶了90千米，设行驶的时间为x（小时），两车之间的距离为y（千米），图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系，根据图象提供的信息，以下选项中正确的个数是（）
①甲乙两地的距离为450千米；②轿车的速度为70千米/小时；③货车的速度为60千米/小时；④点C的实际意义是轿车出发5小时后到达乙地，此时两车间的距离为300千米．

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
8. (2022八上·济南期中) 漏刻是我国古代的一种计时工具，据史书记载，西周时期就已经出现了漏刻，这是中国古代人民对函数思想的创造性应用，小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型，研究中发现水位h(cm)是时间t(min)的一次函数，如下表是小明记录的部分数据，其中有一个h的值记录不符合题意，请排除后利用正确的数据确定当时间t为8时，对应的高度h为（）
t（min）
……
0
1
2
3
……
h（cm）
……
0.7
1.2
1.5
1.9
……

A . 3.3 B . 3.65 C . 3.9 D . 4.7

答案解析收藏纠错 + 选题
9. (2021八上·长清期中) 某品牌鞋子的长度ycm与鞋子的“码”数x之间满足一次函数关系．若22码鞋子的长度为16cm，44码鞋子的长度为27cm，则38码鞋子的长度为（）

A . 23cm B . 24cm C . 25cm D . 26cm

答案解析收藏纠错 + 选题
10. (2021八上·苏州期末) 在数轴上，点 $\text{[math]}$ 表示－2，点 $\text{[math]}$ 表示 $\text{[math]}$ 为数轴上两点，点 $\text{[math]}$ 从点 $\text{[math]}$ 出发以每秒 $\text{[math]}$ 个单位长度的速度向左运动，同时点 $\text{[math]}$ 从点 $\text{[math]}$ 出发以每秒 $\text{[math]}$ 个单位长度的速度向左运动，点 $\text{[math]}$ 到达原点 $\text{[math]}$ 后，立即以原来的速度返回，当点 $\text{[math]}$ 回到点 $\text{[math]}$ 时，点 $\text{[math]}$ 与点 $\text{[math]}$ 同时停止运动．设点 $\text{[math]}$ 运动的时间为 $\text{[math]}$ 秒，点 $\text{[math]}$ 与点 $\text{[math]}$ 之间的距离为 $\text{[math]}$ 个单位长度，则下列图像中表示 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系的是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

11. (2022八上·城阳期中) 如图是A，B两种手机套餐每月资费y(元)与通话时间x(分钟)对应的函数图象，若小红每月通话时间大约为500分钟，则从A，B两种手机资费套餐中选择套餐更合适．

答案解析收藏纠错 + 选题
12. (2024八下·罗定月考) 某长途汽车客运公司规定旅客可免费携带一定质量的行李.当行李的质量超过规定时，需付的行李费y（元）与行李质量 $\text{[math]}$ 之间满足一次函数关系，部分对应值如下表：

$\text{[math]}$

…

30

40

50

…

y（元）

…

4

6

8

…

则旅客最多可免费携带行李的质量是kg.

答案解析收藏纠错 + 选题
13. (2021八上·巴中期末) 如图，已知直线l₁：y＝3x+1和直线l₁：y＝mx+n交于点P（1，b），则关于x，y的二元一次方程组 $\text{[math]}$ 的解是 .

答案解析收藏纠错 + 选题
14. (2022八上·安徽期中) 已知直线y=x+b和y=ax+2交于点P（3，-1），则关于x的方程（a-1）x=b-2的解为．

答案解析收藏纠错 + 选题
15. (2021八上·淳安期末) 如图，一次函数y＝kx+b的图象与x轴交于点A（3，0），与y轴交于点B（0，4），与正比例函数y＝ax的图象交于点C，且点C的横坐标为2，则不等式ax＜kx+b的解集为．

答案解析收藏纠错 + 选题
16. (2021八上·萧山月考) 如图，在平面直角坐标系中，直线 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，直线1垂直平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，点 $\text{[math]}$ 是直线1上且在第一象限一动点．若 $\text{[math]}$ 是等腰三角形，点 $\text{[math]}$ 的坐标是．

答案解析收藏纠错 + 选题

三、解答题（共10题，共72分）

17. (2020八上·蜀山月考) 医药研究所试验某种新药效时，成人如果按剂量服用，血液中每毫升含药量y（毫克）随时间x的变化如图所示，如果每毫升血液中含药量超过4微克（含4微克）时治疗疾病为有效，那么有效时间是多少小时？

答案解析收藏纠错 + 选题
18. (2021八上·连云月考) 如图，在靠墙（墙长为18m）的地方围建一个矩形的养鸡场，另三边用竹篱笆围成，如果竹篱笆总长为35m，求鸡场的长y （m）与宽x （m）的函数关系式，并求自变量的取值范围.

答案解析收藏纠错 + 选题
19. (2022八上·雁塔期中) 某水产养殖户有20吨水产品待售，现有两种销售方式：一是批发，二是零售．经过市场调查，这两种销售方式每天的销量及每吨所获的利润如下表：
销售方式
每天销量/吨
每吨所获利润/元
批发
3
4000
零售
1
6000
假设该养殖户售完20吨水产品，其中批发了x吨，所获总利润为y元．
1. （1）求y与x之间的函数解析式；
2. （2）因为人手紧缺，这个养殖户每天只能采用一种销售方式销售，且正好10天销售完所有水产品，请计算该养殖户所获总利润．
答案解析收藏纠错 + 选题
20. (2024八上·诸暨期末) 随着春节临近，某儿童游乐场推出了甲、乙两种消费卡，其中，甲为按照次数收费，乙为收取办卡费用以后每次打折收费．设消费次数为x时，所需费用为y元，且y与x的函数关系如图所示．根据图中信息，解答下列问题．
1. （1）分别求出选择这两种卡消费时，y关于x的函数表达式；
2. （2）求出入园多少次时，两者花费一样？费用是多少？
3. （3）洋洋爸准备了240元，请问选择哪种划算？
答案解析收藏纠错 + 选题
21. (2022八上·西安月考) 如图1．函数 $\text{[math]}$ 与x轴交于点A，与y轴交于点B，点C与点A关于y轴对称．
1. （1） ①直接写出点C的坐标；
  ②求直线BC的函数解析式；
2. （2）设点M是x轴上的一个动点，过点M作y轴的平行线，交直线AB于点P，交直线BC于点Q．连接BM，如图2，在点M的运动过程中是否存在点P，使∠BMP=∠BAC，若存在，请求出点P坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
22. (2022八上·金华月考) 为了改善我市小区居位环境，构建“精美金华”，市政府持续对老旧小区进行改造，现要将200吨水泥，120吨外墙涂料运往某小区，计划租用甲、乙两种货车共8辆将这批水泥和外墙涂料全部运出，已知一辆甲种货车可装水泥和外墙涂料各20吨，一辆乙种货车可装水泥40吨和外墙涂料10吨．
1. （1）请你设计方案安排甲、乙两种货车可一次性将货物运到目的地，有哪几种方案？
2. （2）若甲种货车每辆要付运输费960元，乙种货车每辆要付运输费1200元，则应选择哪种方案使运输费最少？最少运费是多少？
答案解析收藏纠错 + 选题
23. (2021八上·海曙期末) 我省要按照城市功能特点，城区消费到2022年，建设20个省内特色消费中心，着力发展“夜经济”，打造郑州“夜商都”等地方夜消费品牌升级版．允许市场经营主体在规范有序的条件下，采取“店铺外摆”“露天市场”方式进行销售．个体业主小王响应号召，采取“店铺外摆”方式销售甲、乙两款特价商品，两款商品的进价与售价如表所示：

甲商品

乙商品

进价（元/件）

35

5

售价（元/件）

45

8

小王计划购进甲、乙两种商品共100件进行销售．设小王购进甲商品 $\text{[math]}$ 件，甲、乙商品全部销售完后获得的利润为 $\text{[math]}$ 元．
1. （1）求出 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式；
2. （2）若购进乙商品的件数不少于甲商品件数的3倍，当购进甲，乙两种商品各多少件时，可使得甲、乙商品全部销售完后获得的利润最大？
答案解析收藏纠错 + 选题
24. (2021八上·萧山期末) 某校八年级举行英语演讲比赛，购买A，B两种笔记本作为奖品，这两种笔记本的单价分别是12元和8元．根据比赛设奖情况，需购买笔记本共30本．
1. （1）设买A笔记本n本，买两种笔记本的总费为w元，写出w（元）关于n（本）的函数关系式；
2. （2）若所购买A笔记本的数量要不多于B笔记本数量的 $\text{[math]}$ ，但又不少于B笔记本数量的 $\text{[math]}$ ，购买这两种笔记本各多少时，费用最少？最少的费用是多少元？
3. （3）若学校根据实际除了A，B两种笔记本外，还需一种单价为10元的C笔记本，若购买的总本数不变，C笔记本的数量是B笔记本的数量的2倍，A笔记本的数量不少于B笔记本的数量，试设计一种符合上述条件购买方案，且使所需费用最少．
答案解析收藏纠错 + 选题
25. (2021八上·诸暨期末) 目前，全国各地都在积极开展新冠肺炎疫苗接种工作，某生物公司接到批量生产疫苗任务，要求5天内加工完成22万支疫苗，该公司安排甲，乙两车间共同完成加工任务，乙车间加工过程中停工一段时间维修设备，然后提高效率继续加工，直到与甲车间同时完成加工任务为止，设甲，乙两车间各白生产疫苗y（万支）与甲车间加工时间x（天）之间的关系如图1所示；两车间未生产疫苗W（万支）与甲车间加工时间x（天）之间的关系如图2所示，请结合图象回答下列问题：
1. （1）甲车间每天生产疫苗万支，第一天甲、乙两车间共生产疫苗万支，a＝；
2. （2）当x＝3时，求甲、乙车间生产的疫苗数（万支）之差y₁﹣y₂；
3. （3）若5.5万支疫苗恰好装满一辆货车，那么加工多长时间装满第一辆货车？再加工多长时间恰好装满第三辆货车？
答案解析收藏纠错 + 选题
26. (2021八上·嘉兴期末) 某工厂投资组建了日废水处理量为20吨的废水处理车间，已知该车间处理废水时每天需固定成本30元，并且每处理一吨废水还需费用8元.若该车间在无法完成当天工业废水的处理任务时，需将超出20吨的部分交给第三方企业处理。如图所示为该厂日废水处理总费用y(元)与该厂日产生的工业废水x(吨)之间的函数关系图象.
1. （1）求y关于x的函数关系式：
2. （2）设该厂日废水处理的平均费用为a元/吨，
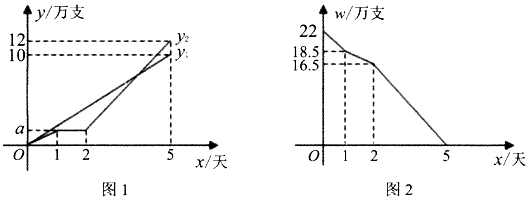
  ①当a=10时，在图1中画出直线y=ax的图象，结合图象判断直线y=ax与日废水处理总费用y的函数图象交点个数，求交点横坐标x的值并说明它的实际意义；
  
  ②当a=t时，参照上一小题的解法，求出该厂这日产生工业废水量x的值.
答案解析收藏纠错 + 选题