巍巍古寺在山林,不知寺内几多僧。三百六十四只碗,看看用尽不差争。 三人共食一碗饭,四人共吃一碗羹。 请问先生明算者,算来寺内几多僧? |
|
意思是:山林中有一座古寺,不知道寺内有多少僧人. 已知一共有364只碗,刚好能够用完. 每三个僧人一起吃一碗饭,每四个僧人一起吃一碗羹. 请问寺内一共有多少僧人?请解答上述问题.


| 售价 | 60 | 65 | 70 |
| 销售量 | 1400 | 1300 | 1200 |
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
销售单价(元) | x |
销售量y(件) |
|
销售玩具获得利润w(元) |
|
|
衬衫价格 |
甲 |
乙 |
|
进价(元 |
|
|
|
售价(元 |
260 |
180 |
若用3000元购进甲种衬衫的数量与用2700元购进乙种衬衫的数量相同.
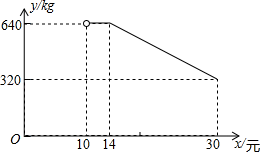

图1

图2
请根据以上要求,完成如下问题:
①设购买A型机器人台,购买总金额为
万元,请写出
与
的函数关系式;
②请你求出最节省的采购方案,购买总金额最低是多少万元?