2023年上海市中考模拟试卷（1）

更新时间：2023-02-03 浏览次数：161 类型：中考模拟

一、单选题（每题4分，共24分）

1. (2023八上·郑州期末) 在实数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， 0.1010010001中，无理数有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题
2. (2023八上·吴忠期末) 关于x的分式方程 $\text{[math]}$ +3＝ $\text{[math]}$ 无解，m的值为（　　）

A . 7 B . -7 C . 1 D . -1

答案解析收藏纠错 + 选题
3. (2022九上·莱州期末) 如图，点B在y轴的正半轴上，点C在反比例函数 $\text{[math]}$ 的图象上，菱形 $\text{[math]}$ 的面积为8，则k的值为（）

A . -4 B . 4 C . -2 D . 2

答案解析收藏纠错 + 选题
4. (2022九上·顺庆月考) 一组数据为7，9，9，11，若添加一个数据9，则发生变化的统计量是（）

A . 方差 B . 众数 C . 中位数 D . 平均数

答案解析收藏纠错 + 选题
5. (2021八下·徐汇期末) 已知四边形 $\text{[math]}$ 中， $\text{[math]}$ ，下列判断中的正确的是（）

A . 如果 $\text{[math]}$ ，那么四边形 $\text{[math]}$ 是等腰梯形 B . 如果 $\text{[math]}$ ，那么四边形 $\text{[math]}$ 是菱形 C . 如果AC平分BD，那么四边形 $\text{[math]}$ 是矩形 D . 如果 $\text{[math]}$ ，那么四边形 $\text{[math]}$ 是正方形

答案解析收藏纠错 + 选题
6. (2022九上·渠县期末) 如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连结BD、DP，BD与CF相交于点H.给出下列结论，其中正确结论的个数是（）
①△BDE∽△DPE；② $\text{[math]}$ ；③ $\text{[math]}$ ；④tan∠DBE= $\text{[math]}$ .

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题（每题4分，共48分）

7. (2023九上·万州期末) 计算 $\text{[math]}$ .

答案解析收藏纠错 + 选题
8. (2022八上·青浦期中) 函数 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
9. (2022八上·岷县开学考) 已知 $\text{[math]}$ ， $\text{[math]}$ 是一次函数 $\text{[math]}$ 的图象上的两个点，则 $\text{[math]}$ ， $\text{[math]}$ 的大小关系是．

答案解析收藏纠错 + 选题
10. (2023九上·韩城期末) 若 $\text{[math]}$ 是关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的一个根，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
11. (2023九上·万州期末) 某一天，小林与小李都要去核酸检测点进行核酸检测，若当地共有A，B，C，D四个核酸检测点，则在随机选择的情况下，两人都在同一检测点进行检测的概率是.

答案解析收藏纠错 + 选题
12. (2022九上·东阳月考) 若将抛物线y＝x²-6x+5所在的平面直角坐标系中的x轴向上平移1个单位，把y轴向右平移2个单位，则该抛物线在新的平面直角坐标系下的函数表达式为．

答案解析收藏纠错 + 选题
13. (2022九上·阳信期中) 为了估计鱼塘中的鱼数，养鱼者首先从鱼塘中打捞100条鱼，在每一条鱼身上做好记号后把这些鱼放归鱼塘，再从鱼塘中打捞10条鱼，如果在这10条鱼中有2条鱼是有记号的，那么估计鱼塘中鱼的条数为条．

答案解析收藏纠错 + 选题
14. (2022·鄂尔多斯) 如图，在△ABC中，AB＝AC＝4，∠CAB＝30°，AD⊥BC，垂足为D，P为线段AD上的一动点，连接PB、PC．则PA+2PB的最小值为．

答案解析收藏纠错 + 选题
15. (2022·长宁模拟) 如图，在△ABC中，点D在边AB上，且 $\text{[math]}$ ＝ $\text{[math]}$ ，点E是AC的中点， $\text{[math]}$ ＝ $\text{[math]}$ ， $\text{[math]}$ ＝ $\text{[math]}$ ，试用向量 $\text{[math]}$ ， $\text{[math]}$ 表示向量 $\text{[math]}$ ，那么 $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题
16. (2022八上·济南期中) 甲、乙两位同学骑自行车，从各自家出发上学，他们离乙家的距离y(km)与出发时间x(min)之间的函数关系如图所示，则乙比甲早到分钟．

答案解析收藏纠错 + 选题
17. (2019七下·黄石期中) 如图，长方形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A（2，0）同时出发，沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2017次相遇地点的坐标是.

答案解析收藏纠错 + 选题
18. (2020九上·勃利期末) 矩形 $\text{[math]}$ 中， $\text{[math]}$ =5， $\text{[math]}$ =12，如果分别以 $\text{[math]}$ ， $\text{[math]}$ 为圆心的两圆相切，点 $\text{[math]}$ 在⊙ $\text{[math]}$ 内，点 $\text{[math]}$ 在⊙ $\text{[math]}$ 外，那么⊙ $\text{[math]}$ 的半径 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题

三、解答题（共7题，共78分）

19. (2020七上·渠县月考) 有理数 $\text{[math]}$ 在数轴上的位置如图所示：化简：

$\text{[math]}$

答案解析收藏纠错 + 选题
20. (2023八上·平南期末) 解不等式组： $\text{[math]}$ ，并利用数轴表示不等式组的解集.

答案解析收藏纠错 + 选题
21. (2020九上·合肥月考) 如图，两幢建筑物AB和CD，AB⊥BD，CD⊥BD，AB=15m， CD=20m。AB和CD之闻有一景观池，小双在A点测得池中喷泉处E点的俯角为42°，在C点测得E点的俯角为45°，点B、E、D在同一直线上。求两幢建筑物之间的距离BD.（结果精确到0.1m）[参考数据： sin42°=0.67，cos42°=0.74，tan42°=0。90]

答案解析收藏纠错 + 选题
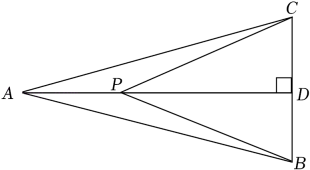
22. (2020八下·绍兴月考) 某连锁超市派遣调查小组在春节期间调查某种商品的销售情况，下面是调查后小张与其他两位成员交流的情况．
小张：“该商品的进价为24元/件．”

成员甲：“当定价为40元/件时，每天可售出480件．”

成员乙：“若单价每涨1元，则每天少售出20件；若单价每降1元，则每天多售出40件．”根据他们的对话，请你求出要使该商品每天获利7680元，应该怎样合理定价？

答案解析收藏纠错 + 选题
23. (2017·浙江模拟)
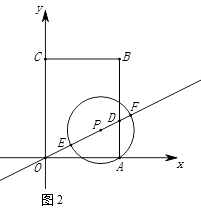
如图所示，梯形ABCD中，AB∥DC，∠B=90°，AD=15，AB=16，BC=12，点E是边AB上的动点，点F是射线CD上一点，射线ED和射线AF交于点G，且∠AGE=∠DAB．
1. （1）求线段CD的长；
2. （2）如果△AEG是以EG为腰的等腰三角形，求线段AE的长；
3. （3）如果点F在边CD上（不与点C、D重合），设AE=x，DF=y，求y关于x的函数解析式，并写出x的取值范围．
答案解析收藏纠错 + 选题
24. (2021·阳西模拟) 如图，点 $\text{[math]}$ ， $\text{[math]}$ 分别在 $\text{[math]}$ 轴和 $\text{[math]}$ 轴的正半轴上， $\text{[math]}$ ， $\text{[math]}$ 的长分别为 $\text{[math]}$ 的两个根 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 轴的负半轴上，且 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求过 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点的抛物线的函数解析式；
2. （2）点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以每秒2个单位长度的速度沿 $\text{[math]}$ 运动到点 $\text{[math]}$ ，点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以每秒1个单位长度的速度沿 $\text{[math]}$ 运动到点 $\text{[math]}$ ，连接 $\text{[math]}$ ，当点 $\text{[math]}$ 到达点 $\text{[math]}$ 时，点 $\text{[math]}$ 停止运动，求 $\text{[math]}$ 的最大值；
3. （3） $\text{[math]}$ 是抛物线上一点，是否存在点 $\text{[math]}$ ，使得 $\text{[math]}$ ？若存在，请求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
25. (2017·瑞安模拟) 如图1，直角坐标系中有一矩形OABC ，其中 O是坐标原点，点A ， C分别在x轴和y轴上，点B的坐标为（3，4），直线 $\text{[math]}$ 交AB于点D ，点P是直线 $\text{[math]}$ 位于第一象限上的一点，连接PA ，以PA为半径作⊙P ，
1. （1）连接AC ，当点P落在AC上时，求PA的长；
2. （2）当⊙P经过点O时，求证：△PAD是等腰三角形；
3. （3）
  设点P的横坐标为m ，
  在点P移动的过程中，当⊙P与矩形OABC某一边的交点恰为该边的中点时，求所有满足要求的m值；
答案解析收藏纠错 + 选题