



解:∵PN⊥OB于点N,
∴∠PNB= ▲ °( )(填推理的依据).
∵PM∥OB,
∴∠MPN=∠PNB=90°,
∠POB= ▲ ( )(填推理的依据).
∵OP平分∠AOB,且∠AOB=60°,
∴∠POB=∠AOB=30°(角的平分线的定义).
∴∠MPO= ▲ °.
∵∠MPO+∠OPN=∠MPN,
∴∠OPN= ▲ °.


已知:如图, ,
.
求证: .
证明:∵ ▲ ( ),
又∵ ,
∴▲ (等量代换).
∴∥▲( ).
∴ ▲
( ).
又∵ ,
∴ .
∴( ).
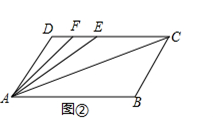
已知:如图,点E在线段的延长线上,点F在线段
的延长线上,连接E,
,
,
.
求证: .

证明:因为( ▲ ),
又因为(已知),
所以(等量代换),
所以(同旁内角互补,两直线平行),
所以( ▲ ),
因为(已知),
所以(等量代换),
所以( ▲ ),
所以( ▲ ).
①若 ,
, 则
▲ ;
②若 , 则
▲ ;
③探究与
之间的数量关系,说明理由;

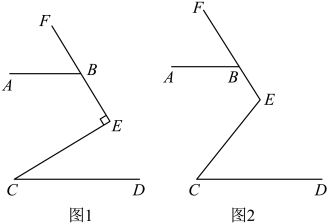

小红:过点作
, 如图2
∵(已知)
∴( )
∴ ▲ , ▲ (两直线平行,内错角相等)
∵(已知)
∴ ▲ (等量代换)
请把小红的证明过程补充完整;

如图1,点P在直线AC右侧时,∠APC﹣(∠A+∠C)=度;
如图2,点P在直线AC左侧时,∠APC+(∠A+∠C)=度;
如图3,点P在直线AC右侧时,∠APC与∠A﹣∠C有怎样的等量关系?写出结论并证明;
如图4,点P在直线AC左侧时,∠APC﹣(∠A﹣∠C)= ▲ 度.
①的值不变;
②∠GEN-∠BDF的值不变.
其中只有一个是正确的,你认为哪个是正确的?讲求出不变的值是多少.




①判断∠AED与α,β的数量关系,并说明理由;
②若M为平面内一动点,且MA∥ED,请直接写出∠MAB与β的数量关系.
