

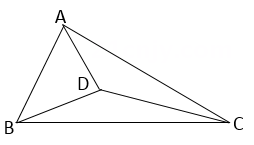


已知:如图, .
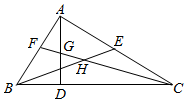
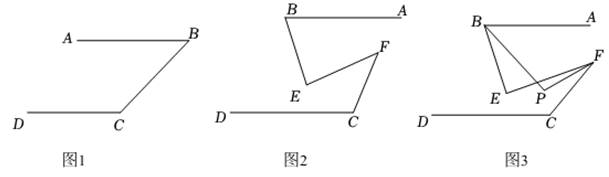
【初步感知】如图1,若 , 求
的度数;
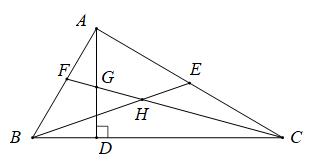
【拓展延伸】如图2,当点、
在两平行线之间,且在位于
异侧时,求证:
;
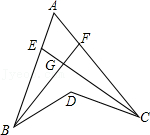
【类比探究】如图3,若 ,
, 若
,
, 直接写出
的度数.
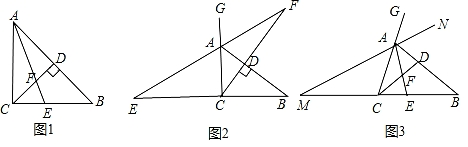
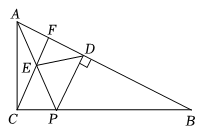
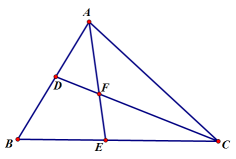
【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
【变式思考】如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
【探究延伸】如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
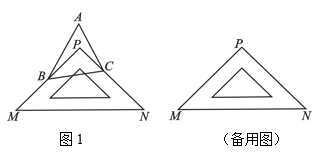
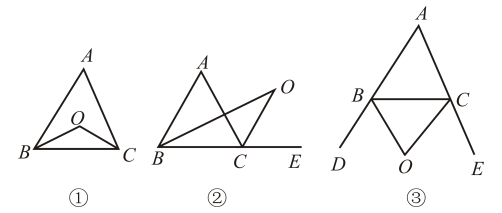
①试探求∠A与的数量关系并证明你的结论;
②按角的大小来判断的形状.