2023年浙教版数学九年级上册3.3 垂径定理同步测试（提...

更新时间：2023-08-01 浏览次数：77 类型：同步测试

一、选择题

1. (2023九上·武义月考) 如图为一座拱形桥示意图，桥身 $\text{[math]}$ （弦 $\text{[math]}$ ）长度为8，半径 $\text{[math]}$ 垂直 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，则桥拱高 $\text{[math]}$ 为（）

A . 3 B . 2.5 C . 2 D . 1.5

答案解析收藏纠错 + 选题
2. (2023九上·吴兴期末) 常用水笔的笔尖是通过顶端的球座口内置一颗可以滚动带墨出水的球珠构成（轴截面如图所示），某工厂生产了一批直径均为 $\text{[math]}$ 的球珠和可以放置球珠的笔尖，要求笔头球珠探出部分的长度h不少于 $\text{[math]}$ 但不超过 $\text{[math]}$ ，以下生产的不同球座口宽度a中符合要求的是（）

A . 0.45 B . 0.35 C . 0.25 D . 0.15

答案解析收藏纠错 + 选题
3. (2023九上·慈溪期末) “圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长六寸，问径几何？”用现代的数学语言表述是：“ $\text{[math]}$ 为 $\text{[math]}$ 的直径，弦 $\text{[math]}$ ，垂足为E， $\text{[math]}$ 寸， $\text{[math]}$ 寸，求直径 $\text{[math]}$ 的长？”依题意得 $\text{[math]}$ 的长为（）

A . 4寸 B . 5寸 C . 8寸 D . 10寸

答案解析收藏纠错 + 选题
4. (2023九上·钱江月考) 点 $\text{[math]}$ 是 $\text{[math]}$ 内一点，过点 $\text{[math]}$ 的最长弦的长为10，最短弦的长为6，则 $\text{[math]}$ 的长为（）

A . 8 B . 2 C . 5 D . 4

答案解析收藏纠错 + 选题
5. (2022九上·平谷期末) “今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”这是《九章算术》中的一个问题，用现代的语言表述为：如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径，弦 $\text{[math]}$ 于E， $\text{[math]}$ 寸，弦 $\text{[math]}$ 寸，则 $\text{[math]}$ 的半径为多少寸（）

A . 5 B . 12 C . 13 D . 26

答案解析收藏纠错 + 选题
6. (2022九上·长兴月考) 如图，AD是⊙O的直径，以A为圆心，弦AB为半径画弧交⊙O于点C，连结BC交AD于点E，若DE=2，BC=8，则⊙O的半径是（）

A . $\text{[math]}$ B . 5 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·孝南期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是弦， $\text{[math]}$ ，半径为4， $\text{[math]}$ .则 $\text{[math]}$ 的长（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·韩城期末) 某公园中央地上有一个大理石球，小明想测量球的半径，于是找了两块厚20cm的砖塞在球的两侧（其中间的截面图如图所示），他量了下两砖之间的距离刚好是80cm，则图中截面圆的半径是（）

A . 80cm B . 70cm C . 60cm D . 50cm

答案解析收藏纠错 + 选题
9. (2024九上·江津期末) 如图所示一个圆柱体容器内装入一些水，截面AB在圆心 $\text{[math]}$ 下方，若 $\text{[math]}$ 的直径为 $\text{[math]}$ ，水面宽 $\text{[math]}$ ，则水的最大深度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022九上·青田期中) 如图，在圆 $\text{[math]}$ 中，弦 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上移动，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 做 $\text{[math]}$ 交圆 $\text{[math]}$ 于点 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023九上·泰兴期末) 如图是一座圆弧型拱桥的截面示意图，若桥面跨度 $\text{[math]}$ 米，拱高 $\text{[math]}$ 米（C为 $\text{[math]}$ 的中点，D为弧 $\text{[math]}$ 的中点）.则桥拱所在圆的半径为米.

答案解析收藏纠错 + 选题
12. (2023九上·凤凰期末) 如图，是一个高速公路的隧道的横截面，若它的形状是以O为圆心的圆的一部分，路面 $\text{[math]}$ 米，拱高 $\text{[math]}$ 米，则此圆的半径 $\text{[math]}$ ＝.

答案解析收藏纠错 + 选题
13. (2023九上·武义期末) 如图， $\text{[math]}$ 的半径 $\text{[math]}$ 垂直于弦 $\text{[math]}$ 于点 $\text{[math]}$ ，连结 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点 $\text{[math]}$ ，连结 $\text{[math]}$ .若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

答案解析收藏纠错 + 选题
14. (2023九上·厦门期末) 如图， $\text{[math]}$ 内接于 $\text{[math]}$ ，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点D，交 $\text{[math]}$ 于点E，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

答案解析收藏纠错 + 选题
15. (2022九上·莱州期末) 已知直线m与半径为5cm的⊙O相切于点P，AB是⊙O的一条弦，且 $\text{[math]}$ ，若AB＝6cm，则直线m与弦AB之间的距离为．

答案解析收藏纠错 + 选题
16. (2022九上·利辛月考) 我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题：“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何？”意思是：今有一圆柱形木材，埋在墙壁中，不知其大小．用锯去锯这木材，锯口深 $\text{[math]}$ 寸，锯道长 $\text{[math]}$ 尺（1尺 $\text{[math]}$ 寸）．问这根圆形木材的直径是寸．

答案解析收藏纠错 + 选题

三、作图题

17. (2023九上·韩城期末) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，点P是 $\text{[math]}$ 上一点，且点P是弦 $\text{[math]}$ 的中点，利用尺规作图法作出弦 $\text{[math]}$ .（不写作法，保留作图痕迹）

答案解析收藏纠错 + 选题

四、解答题

18. (2022九上·海淀期末) 紫砂壶是我国特有的手工制造陶土工艺品，其制作过程需要几十种不同的工具，其中有一种工具名为“带刻度嘴巴架”，其形状及使用方法如图1。当制显艺人把“带刻度嘴巴架”上圆弧部分恰好贴在壶口边界时，就可以保证需要粘贴的壶嘴、壶把、壶口中心在一条直线上．图2是符合题意使用该工具时的示意图．如图3， $\text{[math]}$ 为某紫砂壶的壶口，已知 $\text{[math]}$ ， $\text{[math]}$ 两点在 $\text{[math]}$ 上，直线 $\text{[math]}$ 过点 $\text{[math]}$ ，且 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，求这个紫砂壶的壶口半径 $\text{[math]}$ 的长．

答案解析收藏纠错 + 选题

五、综合题

19. (2023九上·兰溪月考) 根据素材解决问题．

设计货船通过圆形拱桥的方案
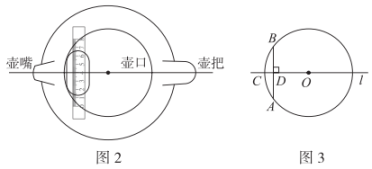
素材1	图1中有一座圆拱石桥，图2是其圆形桥拱的示意图，测得水面宽AB=16m，拱顶离水面的距离CD=4m．
素材2	如图3，一艘货船露出水面部分的横截面为矩形EFGH，测得EF=3m，EH=10m．因水深足够，货船可以根据需要运载货物．据调查，船身下降的高度y(米)与货船增加的载重量x (吨)满足函数关系式y= $\text{[math]}$ x．
问题解决
任务1	确定桥拱半径	求圆形桥拱的半径．
任务2	拟定设计方案	根据图3状态，货船能否通过圆形桥拱？若能，最多还能卸载多少吨货物？若不能，至少要增加多少吨货物才能通过？

答案解析收藏纠错 + 选题

20. (2022九上·青田期中) “筒车”是一种以水流作动力，取水灌田的工具.明朝科学家徐光启在 $\text{[math]}$ 农政全书 $\text{[math]}$ 中用图画描绘了“筒车”的工作原理.如图，“筒车”盛水筒的运行轨迹是以轴心 $\text{[math]}$ 为圆心的圆，已知圆心 $\text{[math]}$ 始终在水面上方，且当圆被水面截得的弦 $\text{[math]}$ 为6米时，水面下盛水筒的最大深度为1米 $\text{[math]}$ 即水面下方部分圆上一点距离水面的最大距离 $\text{[math]}$ .
1. （1）求该圆的半径；
2. （2）若水面上涨导致圆被水面截得的弦 $\text{[math]}$ 从原来的6米变为8米时，则水面下盛水筒的最大深度为多少米？
答案解析收藏纠错 + 选题
21. (2023九上·萧山期中) 如图，⊙O的直径AB垂直于弦CD，垂足为E，AE＝2，CD＝8.
1. （1）求⊙O的半径长；
2. （2）连接BC，作OF⊥BC于点F，求OF的长.
答案解析收藏纠错 + 选题
22. (2022九上·嘉兴期中) 【概念引入】 $\text{[math]}$
在一个圆中，圆心到该圆的任意一条弦的距离，叫做这条弦的弦心距.
1. （1）【概念理解】
  如图1，在 $\text{[math]}$ 中，半径是5，弦 $\text{[math]}$ ，则这条弦的弦心距 $\text{[math]}$ 长为.
2. （2）通过大量的做题探究；小明发现：在同一个圆中，如果两条弦相等，那么这两条弦的弦心距也相等.但是小明想证明时却遇到了麻烦.请结合图2帮助小明完成证明过程如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ .
3. （3）【概念应用】
  如图3，在 $\text{[math]}$ 中 $\text{[math]}$ ， $\text{[math]}$ 的直径为20，且弦 $\text{[math]}$ 垂直于弦 $\text{[math]}$ 于 $\text{[math]}$ ，请应用上面得出的结论求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
23. (2022九上·交城期中) 阅读以下材料，并按要求完成相应的任务．
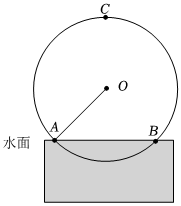
“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题：今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？用现在的数学语言表达是：如图， $\text{[math]}$ 为 $\text{[math]}$ 的直径，弦 $\text{[math]}$ ，垂足为 $\text{[math]}$ ， $\text{[math]}$ 寸， $\text{[math]}$ 尺，其中1尺 $\text{[math]}$ 寸，求出直径 $\text{[math]}$ 的长．
解题过程如下：
连接 $\text{[math]}$ ，设 $\text{[math]}$ 寸，则 $\text{[math]}$ 寸．
∵ $\text{[math]}$ 尺，∴ $\text{[math]}$ 寸．
在 $\text{[math]}$ 中， $\text{[math]}$ ，即 $\text{[math]}$ ，解得 $\text{[math]}$ ，
∴ $\text{[math]}$ 寸．
任务：
1. （1）上述解题过程运用了定理和定理．
2. （2）若原题改为已知 $\text{[math]}$ 寸， $\text{[math]}$ 尺，请根据上述解题思路，求直径 $\text{[math]}$ 的长．
3. （3）若继续往下锯，当锯到 $\text{[math]}$ 时，弦 $\text{[math]}$ 所对圆周角的度数为．
答案解析收藏纠错 + 选题
24. (2022九上·嘉兴期中) 如图，在半径为5的扇形AOB中，∠AOB＝90°，点C是弧AB上的一个动点（不与点A、B重合）OD⊥BC，OE⊥AC，垂足分别为D、E．
1. （1）当BC＝6时，求线段OD的长；
2. （2）在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度；如果不存在，请说明理由．
答案解析收藏纠错 + 选题