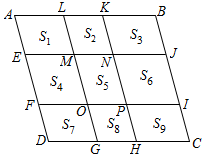

乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )

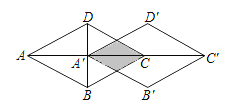




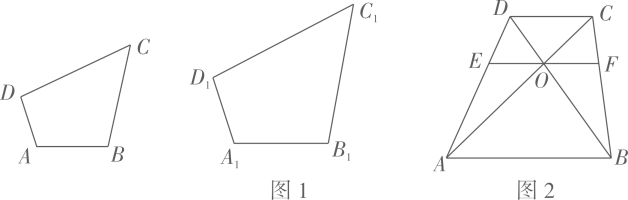
①条边成比例的两个凸四边形相似;(命题)
②三个角分别相等的两个凸四边形相似;(命题)
③两个大小不同的正方形相似.(命题)
同学们有以下思路:
①设新矩形长和宽为x、y , 则依题意 ,
,
联立 得
,再探究根的情况:
根据此方法,请你探究是否存在一个矩形,使其周长和面积都为原矩形的 倍;
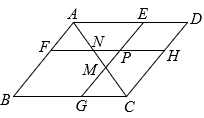
②如图也可用反比例函数与一次函数证明 :
,
:
,那么,
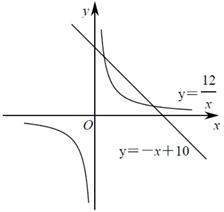
a . 是否存在一个新矩形为原矩形周长和面积的2倍?
b . 请探究是否有一新矩形周长和面积为原矩形的 ,若存在,用图像表达;
c . 请直接写出当结论成立时k的取值范围:.
(定义)四边成比例,且四角分别相等的两个四边形叫做相似四边形.
小明根据探索三角形相似的条件所获得的经验,考虑可以从定义出发逐步弱化条件探究四边形相似的条件.他考虑到“四角分别相等的两个四边形相似”可以举出反例“矩形”,“四边成比例的两个四边形相似”可以举出反例.所以四边形相似的条件必须再添加条件,于是,可以从“四边成比例,且一角对应相等的两个四边形相似”,“三边成比例,且两角分别相等的两个四边形相似”,“两边成比例,且三角分别相等的两个四边形相似”来探究.
学习小组一致认为,“四边成比例,且一角对应相等的两个四边形相似”是真命题,请结合图形完成证明.
已知:四边形 和四边形
中,
,
.
求证:四边形 四边形
.证明:

①“三边成比例,两邻角分别相等且只有一角为其中两边的夹角的两个四边形相似”;
②“三边成比例,两邻角分别相等且都不是其中两边的夹角的两个四边形相似”;
③“三边成比例及其两夹角分别相等的两个四边形相似”;
④“三边成比例,两对角分别相等的两个四边形相似”.
其中真命题是.(填写所有真命题的序号)
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:

请从下列A、B两题中任选一条作答.
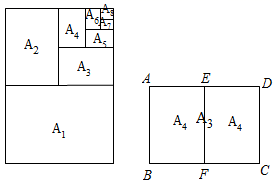
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a=(用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a=(用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a=(用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a=(用含m,n,b的式子表示).